Question

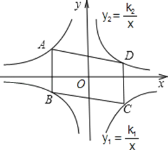
【题目】如图，平行四边形ABCD的顶点为A、C在双曲线y1=上，B、D在双曲线上，k1=2k2（k1＞0），AB∥y轴，=24，则k2的值为（ ）

A.4B.－4C.D.

Answer 1

【答案】A

【解析】

利用平行四边形的性质设A（x，y1）、B（x、y2），根据反比例函数的图象关于原点对称的性可知C（-x，-y1）、D（-x、-y2）；然后由反比例函数图象上点的坐标特征，将点A、B的坐标分别代入它们所在的函数图象的解析式，求得y1=-2y2；最后根据SABCD=|2x|=24可以求得k2=y2x=4．

解：在ABCD中，AB∥CD，AB=CD（平行四边形的对应边平行且相等），故设A（x，y1）、B（x、y2），则根据反比例函数的图象关于原点对称的性质知，C（-x，-y1）、D（-x、-y2）．
∵A在双曲线y1=上，B在双曲线上，
∴x=-，x=,
∴-=；
又∵k1=2k2（k1＞0），
∴y1=-2y2；
∵SABCD=24，
∴|2x|=6|y2x|=24，
解得y2x=±4，
∵双曲线y2=位于第一、三象限，
∴k2=4.

故答案是：A．