Question

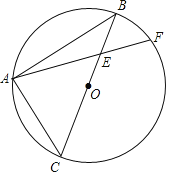
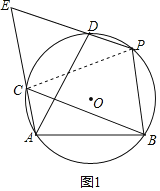
【题目】如图，已知点A、B、P、D、C都在在⊙O上，且四边形BCEP是平行四边形．

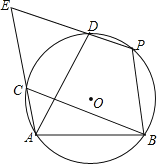
（1）证明：＝；

（2）若AE＝BC，AB＝，的长度是，求EC的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接PC，即可证得∠EPC＝∠PCB，从而证得∠COD＝∠POB，即可证得结论；

（2）根据圆内接四边形的性质得出∠EDC＝∠PBC＝∠PAC，即可证得△APE和△CDE是等边三角形，得出∠PBC＝∠E＝60°，根据平行线的性质得出∠APB＝∠EAP＝60°，即可得出∠AOB＝120°，作OF⊥AB于F，则∠AOF＝∠AOB＝60°，AF＝BF＝AB＝，解直角三角形求得OA＝1，即圆的半径为1，由的长度是得出∠PBD＝15°，即可证得∠DBC＝45°，得到∠DOC＝90°，解等腰直角三角形求得CD＝，由等边三角形的性质得出CE＝CD＝．

（1）证明：连接PC，如图1，

∵四边形BCEP是平行四边形，

∴PE∥BC，∠E＝∠PBC，

∴∠EPC＝∠PCB，

∴＝；

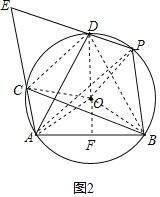
（2）解：如图2，连接AP、BD、CD、OA、OB、OC、OD、OP

∵四边形PBCD是圆内接四边形，四边形APDC是圆内接四边形，

∴∠EDC＝∠PBC＝∠PAC，

∴△APE和△CDE是等边三角形，

∴∠EAP＝60°，

∵PB∥EA，

∴∠APB＝∠EAP＝60°，

∴∠AOB＝120°，

作OF⊥AB于F，则∠AOF＝∠AOB＝60°，AF＝BF＝AB＝，

∴OA＝＝1，

∵的长度是，

∴＝，

∴n＝30°，

∴∠POD＝30°，

∴∠PBD＝15°，

∵∠PBC＝∠E＝60°，

∴∠DBC＝45°，

∴∠DOC＝90°，

∵OC＝OD＝1，

∴CD＝，

∵△ECDs是等边三角形，

∴EC＝CD＝．