题目内容
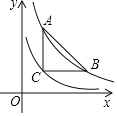
【题目】如图,在平面直角角坐标系中,直线![]() 与双曲线
与双曲线![]() 交于A,C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A,C两点,AB⊥OA交x轴于点B,且OA=AB.
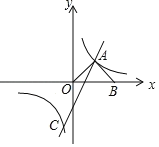
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出关于x的不等式![]() 解集.
解集.
【答案】(1)![]() ;(2)
;(2) ![]() 或
或![]()
【解析】
(1)作高线AD,根据等腰直角三角形的性质和点A的坐标的特点得:x=2x﹣1,可得A的坐标,从而得双曲线的解析式;
(2)联立一次函数和反比例函数解析式得方程组,求解可得点C的坐标,根据图象可得结论.
(1) ∵点A在直线y1=2x-1上,∴设点A(x,2x-1).
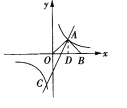
如图,过点A作AD⊥OB于点D.
∵OA=AB,∴OD=BD,又AB⊥OA,∴AD=![]() OB=OD,∴x=2x-1,解得:x=1,∴点A(1,1),又点A(1,1)在双曲线
OB=OD,∴x=2x-1,解得:x=1,∴点A(1,1),又点A(1,1)在双曲线![]() 上,∴k=1×1=1.
上,∴k=1×1=1.
∴双曲线的解析式为![]()
(2)联立直线和双曲线的解析式,得: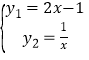 ,解得:
,解得:![]() 或
或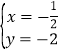 ,∴点C的坐标为(
,∴点C的坐标为(![]() ,-2).
,-2).
观察图像可得:当![]() 或0<x<1,
或0<x<1,![]() ,即关于x的不等式
,即关于x的不等式![]() 的解集是
的解集是![]() 或0<x<1.
或0<x<1.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
【题目】雾霾天气严重影响市民的生活质量。在今年寒假期间,某校九年级一班的综合实践小组学生对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了下图所示的不完整的统计图表:
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 |
|
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) |
|
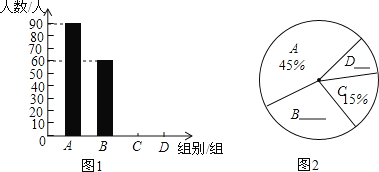
请根据统计图表回答下列问题:
(1)本次被调查的市民共有多少人?并求![]() 和
和![]() 的值;
的值;
(2)请补全条形统计图,并计算扇形统计图中扇形区域![]() 所对应的圆心角的度数;
所对应的圆心角的度数;
(3)若该市有100万人口,请估计市民认为“工业污染和汽车尾气排放是雾霾天气主要成因”的人数.