题目内容
【题目】阅读理解:如果两个正数a,b,即a>0,b>0,有下面的不等式:![]() ,当且仅当a=b时取到等号我们把
,当且仅当a=b时取到等号我们把![]() 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把![]() 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
初步探究:(1)已知x>0,求函数y=x+![]() 的最小值.
的最小值.
问题迁移:(2)学校准备以围墙一面为斜边,用栅栏围成一个面积为100m2的直角三角形,作为英语角,直角三角形的两直角边各为多少时,所用栅栏最短?
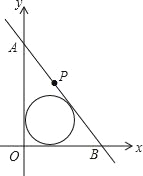
创新应用:(3)如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
【答案】初步探究:(1)4;问题迁移:(2)x=10![]() m时,y有最小值,即所用栅栏最短;创新应用:(3)R=2.
m时,y有最小值,即所用栅栏最短;创新应用:(3)R=2.
【解析】
(1)根据x>0,令a=x,b=![]() ,利用题中的新定义求出函数的最小值即可;
,利用题中的新定义求出函数的最小值即可;
(2)设一直角边为xm,则另一直角边为![]() m,栅栏总长为ym,根据题意表示出y与x的函数关系式,利用题中的新定义求出y取得最小值时x的值即可;
m,栅栏总长为ym,根据题意表示出y与x的函数关系式,利用题中的新定义求出y取得最小值时x的值即可;
(3)设直线AB解析式为y=kx+b,把P坐标代入用k表示出b,进而表示出A与B坐标,确定出OA与OB的长,得出三角形AOB面积,利用题中的新定义求出三角形AOB面积最小时k的值,确定出直角三角形三边,即可求出三角形AOB内切圆半径.
解:(1)令a=x,b=![]() (x>0),
(x>0),
由a+b≥2![]() ,得y=x+
,得y=x+![]() ≥2
≥2![]() =4,
=4,
当且仅当x=![]() 时,即x=2时,函数有最小值,最小值为4;
时,即x=2时,函数有最小值,最小值为4;
(2)设一直角边为xm,则另一直角边为![]() m,栅栏总长为ym,
m,栅栏总长为ym,
y=x+![]() ,
,
当且仅当x=![]() 时,即x=10
时,即x=10![]() m时,y有最小值,即所用栅栏最短;
m时,y有最小值,即所用栅栏最短;
(3)设直线AB的解析式是y=kx+b,
把P(3,4)代入得:4=3k+b,
整理得:b=4﹣3k,
∴直线AB的解析式是y=kx+4﹣3k,
当x=0时,y=4﹣3k;当y=0时,x=![]() ,
,
即A(0,4﹣3k),B(![]() ,0),
,0),
∴S△AOB=![]() OBOA=
OBOA=![]() (4﹣3k)
(4﹣3k)![]() =12﹣(
=12﹣(![]() ),
),
∵要使△AOB的面积最小,
∴![]() 必须最大,
必须最大,
∵k<0,
∴﹣k>0,
∵![]() =2×6=12,当且仅当
=2×6=12,当且仅当![]() 时,取等号,
时,取等号,
解得:k=±![]() ,
,
∵k<0,
∴k=﹣![]() ,
,
即OA=4﹣3k=8,OB=6,
根据勾股定理得:AB=10,
设三角形AOB的内切圆的半径是R,
由三角形面积公式得:![]() ×6×8=
×6×8=![]() ×6R+
×6R+![]() ×8R+
×8R+![]() ×10R,
×10R,
解得:R=2.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案