题目内容
【题目】二次函数y=ax2+bx+c（a≠0）的图象经过点A（3，0），B（2，﹣3），并且以x=1为对称轴．
（1）求此函数的解析式；
（2）作出二次函数的大致图象；
（3）在对称轴x=1上是否存在一点P，使△PAB中PA=PB？若存在，求出P点的坐标；若不存在，说明理由．
【答案】（1）解析式为y=x2﹣2x﹣3；（2）画图见解析；（3）存在，点P的坐标为（1，﹣1）．
【解析】试题分析：（1）根据对称轴的公式x=
和函数的解析式，将
=1和A（3，0），B（2，﹣3）代入函数解析式，组成方程组解答即可；
（2）求出图象与坐标轴的交点坐标，描点即可；
（3）根据两点之间距离公式解答即可．
试题解析：解：（1）根据题意得： 
，解得：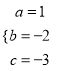 
，∴解析式为y=x2﹣2x﹣3；
（2）二次函数图象如图：
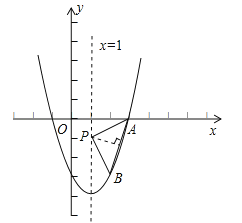
（3）存在．作AB的垂直平分线交对称轴x=1于点P，连接PA、PB，则PA=PB，设P点坐标为（1，m）．∵PA=PB，∴22+m2=（﹣3﹣m）2+1，解得：m=﹣1，∴点P的坐标为（1，﹣1）．
【题目】某学校准备购买A、B两种型号篮球，询问了甲、乙两间学校了解这两款篮球的价格，下表是甲、乙两间学校购买A、B两种型号篮球的情况：
购买学校 | 购买型号及数量（个） | 购买支出款项（元） | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
（1）求A、B两种型号的篮球的销售单价；
（2）若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个，求A种型号的篮球最少能采购多少个？
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表：
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分，求x和y的值；
(2)在(1)的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．
