题目内容
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.
已知:△ABC.
求作:BC边上的高线.
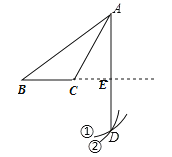
作法:如图,
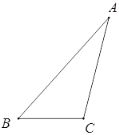
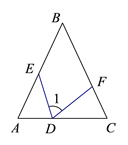
①以点C为圆心,CA为半径画弧;
②以点B为圆心,BA为半径画弧,两弧相交于点D;
③连接AD,交BC的延长线于点E.
所以线段AE就是所求作的BC边上的高线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵CA=CD,
∴点C在线段AD的垂直平分线上( ) (填推理的依据).
∵ = ,
∴点B在线段AD的垂直平分线上.
∴ BC是线段AD的垂直平分线.
∴AD⊥BC.
∴AE就是BC边上的高线.
【答案】补全图形见解析;到线段两个端点距离相等的点在线段的垂直平分线上;BA BD.
【解析】
(1)根据题目中的作图步骤补全图形即可.
(2)由作法得CA=CD,BA=BD,则点B、C在AD的垂直平分线上,即可证明AE就是BC边上的高线.
(1)如图所示:
(2)证明:∵CA=CD,
∴点C在线段AD的垂直平分线上(到线段两个端点距离相等的点在线段的垂直平分线上) (填推理的依据).
∵BA = BD.
∴点B在线段AD的垂直平分线上.
∴ BC是线段AD的垂直平分线.
∴AD⊥BC.
∴AE就是BC边上的高线.

【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)的关系如表所示:
(元)的关系如表所示:
每千克售价 | 25 | 30 | 40 |
每周销售量 | 240 | 200 | 150 |
(1)求出每周销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)的函数关系式.
(元)的函数关系式.
(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否达到每周获利2000元?说明理由.