题目内容
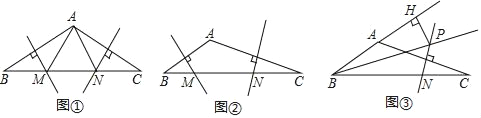
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD= ![]() AE2;④S△ABC=4S△ADF . 其中正确的有( )
AE2;④S△ABC=4S△ADF . 其中正确的有( ) 
A.1个
B.2 个
C.3 个
D.4个
【答案】D
【解析】解:∵在△ABC中,AD和BE是高, ∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD= ![]() AB,
AB,
∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,
∵点F是AB的中点,
∴FE= ![]() AB,
AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中, 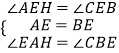 ,
,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD~△BCE,
∴ ![]() =
= ![]() ,即BCAD=ABBE,
,即BCAD=ABBE,
∵ ![]() AE2=ABAE=ABBE,BCAD=ACBE=ABBE,
AE2=ABAE=ABBE,BCAD=ACBE=ABBE,
∴BCAD= ![]() AE2;③正确;
AE2;③正确;
∵F是AB的中点,BD=CD,∴
S△ABC=2S△ABD=4S△ADF . ④正确;
故选:D.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
相关题目