题目内容
【题目】一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.

【答案】当∠C为钝角时,![]() ; 当∠B为钝角时,
; 当∠B为钝角时,![]()
【解析】
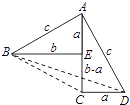
试题(3)如图过A作AD⊥BC于D,则BD=BC+CD=a+CD

在△ABD中:AD2=AB2-BD2
在△ACD中:AD2=AC2-CD2
AB2-BD2= AC2-CD2
c2-(![]() +CD)2= b2-CD2
+CD)2= b2-CD2
∴![]()
∵![]() >0,CD>0
>0,CD>0
∴![]() ,所以:
,所以:![]()
在△ABC中,BC=a=3,CA=b=4,AB=c;若△ABC是钝角三角形 , 当∠C为钝角时,![]() ,c<a+b=7,所以
,c<a+b=7,所以![]() ;
;
当∠B为钝角时,![]() ,解得
,解得![]() ,又因为c>b-a=1,所以
,又因为c>b-a=1,所以![]()

练习册系列答案
相关题目