题目内容
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
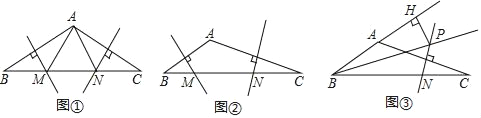
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.
【答案】1200
【解析】
(1)先求出∠AMN=60°,再利用垂直平分线求出∠B=30°,同理求出∠C=30°,最后利用三角形内角和定理即可得出结论;
(2)先判断出∠B+∠C=45°,进而求出∠MAN=90°,即可得出结论;
(3)先判断出Rt△APH≌Rt△CPE,进而判断出Rt△BPH≌Rt△BPE,即可得出结论.
解:(1)如图①,∵△AMN是等边三角形,
∴∠AMN=60°,
∵MG是AB的垂直平分线,
∴AM=AM,
∴∠B=∠BAM=30°
同理:∠C=30°,
∴∠BAC=180°-∠B-∠C=120°
故答案为120;
(2)如图①,连接AM、AN
∵∠BAC=135°
∴∠B+∠C=45°,
又∵点M在AB的垂直平分线上
∴AM=BM
∴∠BAM=∠B,
同理AN=CN,∠CAN=∠C
∴∠BAM+∠CAN=45°
∴∠MAN=90°,
∴AM2+AN2=MN2;
∴BM2+CN2=MN2;

(3)如图②,连接AP、CP,过点P作PE⊥BC于点E
∵BP平分∠ABC,PH⊥BA,PE⊥BC
∴PH=PE
∵点P在AC的垂直平分线上
∴AP=CP
在Rt△APH和Rt△CPE中
![]()
∴Rt△APH≌Rt△CPE
∴AH=CE,
∵BP平分∠ABC,PH⊥BA,PE⊥BC
∴∠HBP=∠CBP,∠BHP=∠BEP=90°
∵BP=BP
∴Rt△BPH≌Rt△BPE
∴BH=BE,
∴BC=BE+CE=BH+CE=AB+2AH
∴AH=(BC-AB)÷2=3.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号 | 月租费(元) | 免费时间(分) | 超过免费时间的通话费(元/分) |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱.




