Question

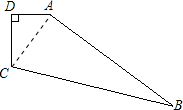
如图，在四边形ABCD中，∠D=90°，AB=12，BC=13，CD=4，AD=3，求四边形ABCD的面积．

Answer 1

连接AC．
在△ADC中，
∵∠D=90°，
∴AC²=AD²+CD²（勾股定理）．
由CD=4，AD=3，
得AC=

AD2+CD2

=

32+42

=5，
在△ABC中，
∵AB=12，BC=13，
∴BC²-AB²=13²-12²=25，
得：BC²=AB²+AC²，
∴∠CAB=90°（勾股定理的逆定理）．
因此，S_{四边形ABCD}=S_△ACD+S_△ACB
=

1

2

AD•DC+

1

2

AB•AC
=

1

2

×3×4+

1

2

×12×5
=36．