Question

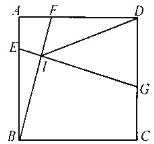
【题目】如图，在边长为6的正方形ABCD中，点E、F、G分别在边AB、AD、CD上，EG与BF交于点I，AE=2，BF=EG，DG>AE，则DI的最小值为________.

Answer 1

【答案】

【解析】

过点E作EM⊥CD于点M，取BE的中点O，连接OI、OD，根据HL证明Rt△BAF≌Rt△EMG，可得∠ABF=∠MEG，所以再证明∠EPF=90°，由直角三角形斜边上的中线等于斜边的一半可得OI=BE，由OD-OI≤DI，当O、D、I共线时，DI有最小值，即可求DI的最小值．

如图，过点E作EM⊥CD于点M，取BE的中点O，连接OI、OD，

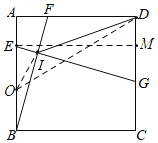
∵四边形ABCD是正方形，

∴AB=AD，∠A=∠D=∠DME=90°，AB∥CD，

∴四边形ADME是矩形，

∴EM=AD=AB，

∵BF=EG，

∴Rt△BAF≌Rt△EMG（HL），

∴∠ABF=∠MEG，∠AFB=∠EGM，

∵AB∥CD

∴∠MGE=∠BEG=∠AFB

∵∠ABF+∠AFB=90°

∴∠ABF+∠BEG=90°

∴∠EIF=90°，

∴BF⊥EG；

∵△EIB是直角三角形，

∴OI=BE，

∵AB=6，AE=2，

∴BE=6-2=4，OB=OE=2，

∵OD-OI≤DI，

∴当O、D、I共线时，DI有最小值，

∵IO=BE=2，

∴OD==2，

∴ID=2-2，即DI的最小值为2-2，

故答案为：2-2.