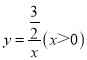Question

【题目】 定义：在凸四边形中，我们把两组对边乘积的和等于对角线的乘积的四边形称为“完美四边形”

（1）在正方形、矩形、菱形中，一定是“完美四边形”的是______．

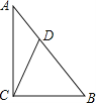
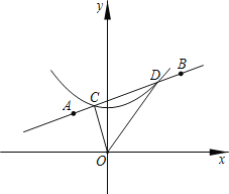
（2）如图1，在△ABC中，AB=2，BC=，AC=3，D为平面内一点，以A、B、C、D四点为顶点构成的四边形为“完美四边形”，若DA，DC的长是关于x的一元二次方程x2-(m+3)x+(5m2-2m+13)=0(其中m为常数)的两个根，求线段BD的长度．

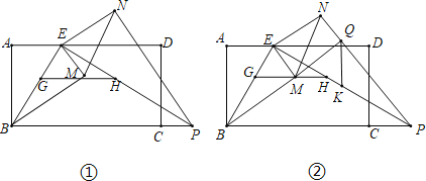
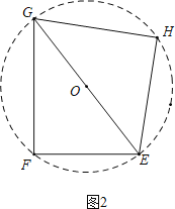
（3）如图2，在“完美四边形”EFGH中，∠F=90°，EF=6，FG=8，求“完美四边形”EFGH面积的最大值．

Answer 1

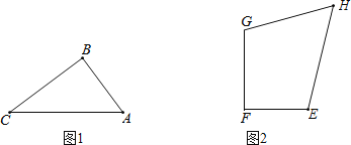
【答案】（1）正方形、矩形；（2）3；（3）49．

【解析】

（1）根据“完美四边形”的定义即可判断．

（2）利用一元二次方程的根的判别式求出m的值，推出AD=DC=2，判断出点D的位置即可解决问题．

（3）由完美四边形的定义以及托勒密定理的逆定理可知：四边形EFGH是圆的内接四边形，圆心是EC的中点O．当点H是的中点时，△EGH的面积最大，此时四边形EFGH的面积最大．

解：（1）根据完美四边形的定义，可知“正方形”、“矩形”是完美四边形．

故答案为：“正方形”、“矩形”．

（2）∵关于x的一元二次方程x2-(m+3)x+(5m2-2m+13)=0，有实数根，

∴△=(m+3)2-4×(5m2-2m+13)=-4(m-1)2≥0，

∴m=1，△=0，

∴方程为：x2-4x+4=0，

∴x1=x2=2，

∴AD=DC=2，

当点D在AC的下方，如图1中，

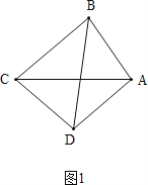
∵四边形ABCD是完美四边形，

∴BDAC=CDAB+BCAD，

∴3BD=4+5，

∴BD=3．

当点D在AC上方时，点D在线段BC上，不符合题意．

∴满足条件的BD的长为3；

（3）如图2中，

由完美四边形的定义以及托勒密定理的逆定理可知：四边形EFGH是圆的内接四边形，圆心是EC的中点O．

∵∠EFG=90°，EF=6，FG=8，

∴EG==10，

当点H是的中点时，△EGH的面积最大，此时四边形EFGH的面积最大，

∴HG=HE=5，

∴四边形的面积的最大值=×6×8+×5×5=49．