题目内容
【题目】如图,一次函数y=-x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数![]() 图象交于点P(2,n).
图象交于点P(2,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在异与点P的另一点C,使得△OBC与△OBP的面积相等?若存在,请求出C点的坐标;若不存在,请说明理由.
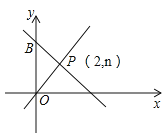
【答案】(1)m的值为5,n的值为3.(2)5;(3)点C的坐标为(﹣2,﹣3).
【解析】试题(1)先把P(2,n)代入y=![]() x即可得到n的值,从而得到P点坐标为(2,3),然后把P点坐标代入y=-x+m可计算出m的值;
x即可得到n的值,从而得到P点坐标为(2,3),然后把P点坐标代入y=-x+m可计算出m的值;
(2)先利用一次函数解析式确定B点坐标,然后根据三角形面积公式求解即可;
(3)根据△OBC与△OBP有一条公共边,可知点C横坐标的绝对值与点P横坐标的绝对值相等,根据题意即可确定出点C的横坐标,代入解析式即可得到点C的坐标.
试题解析:(1)∵点P(2,n)在正比例函数y=![]() x图象上,
x图象上,
∴n=![]() ×2=3,
×2=3,
∴点P的坐标为(2,3),
∵点P(2,3)在一次函数y=﹣x+m的图象上,
∴3=﹣2+m,解得:m=5,
∴一次函数解析式为y=﹣x+5,
∴m的值为5,n的值为3;
(2)当x=0时,y=﹣x+5=5,
∴点B的坐标为(0,5),
∴S△POB=![]() OBxP=
OBxP=![]() ×5×2=5;
×5×2=5;
(3)存在,
∵S△OBC=![]() OB|xC|=S△POB=5,
OB|xC|=S△POB=5,
∴xC=﹣2或xC=2(舍去),
当x=﹣2时,y=![]() ×(﹣2)=﹣3,
×(﹣2)=﹣3,
∴点C的坐标为(﹣2,﹣3).

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目