题目内容
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】根据已知条件利用HL易证△APR≌△APS,再利用全等三角形的性质可得∠PAR=∠PAS,AR=AS,从而可证(1)、(2)正确;由AQ=PQ,利用等边对等角易得∠1=∠APQ,再利用三角形外角的性质可得∠PQC=2∠1,而(1)中PA是∠BAC的角平分线可得∠BAC=2∠1,等量代换,从而有∠PQC=∠BAC,利用同位角相等两直线平行可得QP∥AR,(3)正确;根据已知条件可知△BRP与△CSP只有一角、一边对应相等,故不能证明两三角形全等,因此(4)不正确.
解:(1)PA平分∠BAC.∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴△APR≌△APS,∴∠PAR=∠PAS,∴PA平分∠BAC;
(2)由(1)中的全等也可得AS=AR;
(3)如图所示
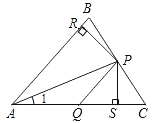
∵AQ=PR,∴∠1=∠APQ,∴∠PQS=∠1+∠APQ=2∠1,又∵PA平分∠BAC,∴∠BAC=2∠1,∴∠PQS=∠BAC,∴PQ∥AR;
(4)∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP,∵PR=PS,∴△BRP不一定全等与△CSP(只具备一角一边的两三角形不一定全等).故选B.
“点睛“本题考查了全等三角形的判定和性质;做题时利用了平行线的判定、等边对等角、三角形外角的性质,要熟练掌握这些知识并能灵活应用.

【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.