题目内容
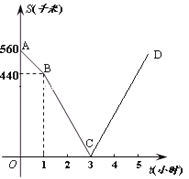
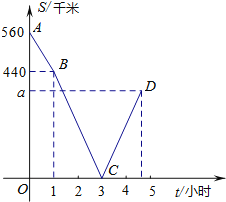
【题目】甲、乙两车分别从M、N两地相向而行，甲车出发1小时后乙车才出发，并以各自速度匀速行驶，甲车出发3小时两车相遇，相遇后两车仍按原速度原方向各自行驶．如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间
(小时)之间的函数图象．则：
①M、N两地之间的距离为________________千米；
②当
时，
__________________小时．
【答案】560 
或
．
【解析】
（1）根据图象，甲出发时的S值即为M、N两地间的距离；（2）设D点表示甲车到达N地，a表示甲车到达D点时与乙车的距离，先求出甲车的速度，然后设乙车的速度为xkm/h，再利用相遇问题列出方程求解即可；然后求出相遇后甲车到达N地的时间，再根据路程=速度×时间求出两车的相距距离a，即可求出D点坐标，设直线BC的解析式为S=k1t+b1（k1≠0），利用待定系数法求出直线BC的解析式，再令S=50，求出t的值；设直线CD的解析式为S=k2t+b2（k2≠0），利用待定系数法求出直线CD的解析式，再令S=50，求出t的值，进而得出答案．
（1）∵t=0时，S=560，
∴M、N两地的距离为560千米
（2）甲车的速度为：（560-440）÷1=120km/h，
设乙车的速度为xkm/h，
则（120+x）×（3-1）=440，
解得x=100；
相遇后甲车到达N地的时间为：（3-1）×100÷120=
（小时），
∴a=（120+100）×=
千米；
∴点D的横坐标为+3=
，即D点坐标为（，），
设直线BC的解析式为S=k1t+b1（k1≠0），
将B（1，440），C（3，0）代入得，
，
解得：k1=-220，b1=660，
所以，S=-220t+660，
当-220t+660=50时，解得：t=，
设直线CD的解析式为S=k2t+b2（k2≠0），
将C（3，0），D（，）代入得：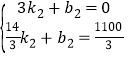
，
解得：k2=220，b2=-660，
所以，S=220t-660（3≤t≤）
当220t-660=50时，解得t=
，
故答案为：①560；②或
