题目内容
【题目】如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标（0，﹣1）．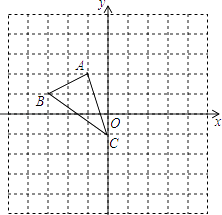
（1）作出△ABC关于原点对称的△A1B1C1 ， 并写出点A1的坐标；
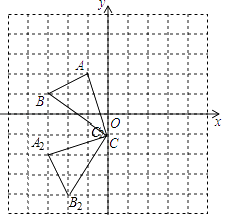
（2）把△ABC绕点C逆时针旋转90°，得△A2B2C，画出△A2B2C，并写出点A2的坐标；
（3）直接写出△A2B2C的面积．
【答案】
（1）
解：如图所示：
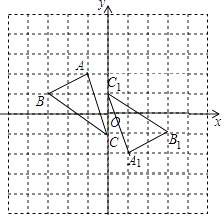
点A1的坐标为：（1，﹣2）；
（2）
解：如图所示：点A2的坐标为：（﹣3，﹣2）；
（3）
解：△A2B2C2的面积=3×3﹣ 
×1×3﹣ ×2×1﹣ ×3×2= 
．
【解析】（1）根据关于原点对称点的性质得出A，B，C对应点，进而得出答案；（2）根据平面直角坐标系写出点A2的坐标即可．（3）利用面积的和差求解：把三角形ABC的面积看作一个正方形的面积减去三个直角三角形的面积．
【考点精析】解答此题的关键在于理解关于原点对称的点的坐标的相关知识，掌握两个点关于原点对称时，它们的坐标的符号相反，即点P（x，y）关于原点的对称点为P’（-x，-y）．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
【题目】九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元，设售价为x元．
（1）请用含x的式子表示：
①销售该运动服每件的利润是 （）元；
②月销量是 （）件；（直接写出结果）
（2）设销售该运动服的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？
（3）若销售该运动服所得的月利润不低于8000元，请确定售价x的取值范围．
