Question

【题目】如图，直线y=x﹣4与x轴、y轴分别交于M、N两点，⊙O的半径为2，将⊙O以每秒1个单位的速度向右作平移运动，当移动时间秒时，直线MN恰好与圆相切．

Answer 1

【答案】4﹣2 或4+2
【解析】解：作EF平行于MN，且与⊙O切，交x轴于点M，交y轴于点N，如图所示．
设直线MN的解析式为y=x+b，即x﹣y+b=0，
∵MN与⊙O相切，且⊙O的半径为2，
∴ = |b|=2，
解得：b=2 或b=﹣2 ，
∴直线MN的解析式为y=x+2 或y=x﹣2 ，
∴点M的坐标为（2 ，0）或（﹣2 ，0）．
令y=x﹣4中y=0，则x=4，
∴点M（4，0）．
∵根据运动的相对性，且⊙O以每秒1个单位的速度向右作平移运动，
∴移动的时间为4﹣2 秒或4+2 秒．
故答案为：4﹣2 或4+2 ．

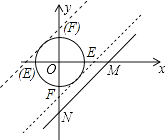
作EF平行于MN，且与⊙O切，交x轴于点M，交y轴于点N，设直线MN的解析式为y=x+b，由⊙O与直线MN相切依据点到直线的距离即可得出关于b的含绝对值符号的一元一次方程，解方程即可求b值，从而得出点E的坐标，根据运动的相对性，即可得出结论．