题目内容
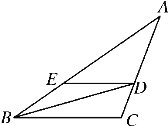
【题目】如图，BD是∠ABC的平分线，DE∥CB，交AB于点E，∠A＝45°，∠BDC＝60°.求△BDE各内角的度数．
【答案】△BDE各内角的度数分别为：∠EBD=15°，∠EDB=15°，∠BED=150°.
【解析】
根据三角形的外角与内角的关系可得∠EBD=15°，再根据DE//CB，BD是∠ABC的平分线，可得∠EDB=15°，再根据三角形的内角和定理即可得∠BED=150°.
∵∠BDC=∠A+∠ABD（△ABD外角=两内角之和），
∴∠ABD=∠BDC-∠A=60°-45°=15°，
∵DE//CB，
∴∠CBD=∠EBD（内错角相等），
又∵BD是∠ABC的平分线，
∴∠CBD=∠BDE，
∴∠EDB=∠EBD=15°，
∴∠BED=180°-∠EBD=∠EDB=180°-15°-15°=150°，
综上所述，△BDE各内角的度数分别为：∠EBD=15°，∠EDB=15°，∠BED=150°.
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？
