题目内容
【题目】如图:直线y=-x+5分别与![]() 轴、
轴、![]() 轴交于A、B两点.
轴交于A、B两点.
(1)求A、B两点的坐标;
(2)已知点C坐标为(4,0),设点C关于直线AB的对称点为D,请直接写出点D的坐标;
(3)请在直线AB找一点M和![]() 轴上找一点N,使△CMN的周长最短,求出点N的坐标和△CMN的周长.
轴上找一点N,使△CMN的周长最短,求出点N的坐标和△CMN的周长.

【答案】(1)A(5,0);B(0,5);(2)D(5,1);(3)N(0,![]() )
)![]() ;
;
【解析】
(1)令x=0,则y=5;令y=0,则x=5,即可求得;(2)首先根据直线AB的解析式可知△OAB是等腰直角三角形,然后根据轴对称的性质即可求出点D的坐标;(3)作出点C关于直线y轴的对称点C′,连接DE交AB于点M,交y轴于点N,则此时△CMN的周长最短.由D、E两点的坐标利用待定系数法求出直线DC′的解析式,再根据y轴上点的坐标特征,即可求出点N的坐标.
(1) ∵直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于A、B两点
轴交于A、B两点
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]()
∴点A坐标为(5,0)、点B 坐标为(0, 5);
(2)如图:过A作直线l⊥x轴,作CD⊥AB交直线l于D,
∵OA=OB=5,
∴∠OAB=45°,
∵CD⊥AB,直线l⊥x轴,
∴∠DCA=45°,∠DAB=45°
∴∠CDA=45°,
∴AD=AC,
∵AB⊥CD,
∴AB垂直平分CD,
∴D即是C关于AB的对称点,
∵A(5,0),C(4,0)
∴AC=AD=1,
∴ 点C 关于直线AB的对称点D的坐标为(5,1),
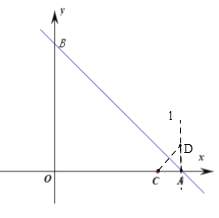
(3) 作点C关于![]() 轴的对称点C′,则C′的坐标为(-4,0)
轴的对称点C′,则C′的坐标为(-4,0)
连接C′D交AB于点M,交![]() 轴于点N,
轴于点N,
∵点C、C′关于![]() 轴对称
轴对称
∴NC= NC′,
∵点C、D关于直线AB对称,
∴CM=DM,
此时,△CMN的周长=CM+MN+NC= DM +MN+ NC′= DC′周长最短;
设直线C′D的解析式为![]()
∵点C′的坐标为(-4,0),点D的坐标为(5,1)
∴![]() ,解得
,解得![]()
∴直线C′D的解析式为![]() ,
,
与![]() 轴的交点N的坐标为 (0,
轴的交点N的坐标为 (0,![]() )
)
根据勾股定理,或两点间距离公式可求 △CMN的周长![]()

 名校课堂系列答案
名校课堂系列答案【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:
①销售该运动服每件的利润是 ()元;
②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
(3)若销售该运动服所得的月利润不低于8000元,请确定售价x的取值范围.