Question

【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　 　．

【答案】3或6

【解析】试题分析：

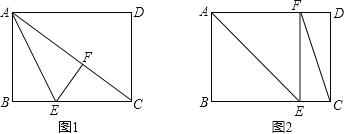
由题意可知有两种情况，见图1与图2；

图1：当点F在对角线AC上时，∠EFC=90°，

∵∠AFE=∠B=90°，∠EFC=90°，

∴点A、F、C共线，

∵矩形ABCD的边AD=8，

∴BC=AD=8，

在Rt△ABC中，AC==10，

设BE=x，则CE=BC﹣BE=8﹣x，

由翻折的性质得，AF=AB=6，EF=BE=x，

∴CF=AC﹣AF=10﹣6=4，

在Rt△CEF中，EF2+CF2=CE2，

即x2+42=（8﹣x）2，

解得x=3，

即BE=3；

图2：当点F落在AD边上时，∠CEF=90°，

由翻折的性质得，∠AEB=∠AEF=×90°=45°，

∴四边形ABEF是正方形，

∴BE=AB=6，

综上所述，BE的长为3或6．

故答案为：3或6．

考点：1、轴对称（翻折变换）；2、勾股定理

【题型】填空题
【结束】
15

【题目】计算：()﹣2﹣+（﹣4）0﹣cos45°．

Answer 1

【答案】1

【解析】试题分析：把原式的第一项根据负整数指数幂的意义化简，第二项根据算术平方根的定义求出9的算术平方根，第三项根据零指数公式化简，最后一项利用特殊角的三角函数值化简，合并后即可求出值.

试题解析：原式=4﹣3+1﹣

=2﹣1

=1．