题目内容
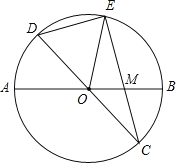
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=![]() .
.
(1)求证:AMMB=EMMC;
(2)求EM的长;
(3)求sin∠EOB的值.
【答案】(1)证明见解析(2)4(3)![]()
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.
【题型】解答题
【结束】
21
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

【答案】(1)见解析;(2)45°;(3)![]()
【解析】试题分析:(1)根据参加生态环保的人数以及百分比求得总人数,用总人数乘以“社区服务”百分比求得其人数,即可解决问题;
(2)根据圆心角=360°×百分比,计算即可;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们参加同一服务活动的情况,再利用概率公式求解即可求得答案.
试题解析:(1)该班全部人数:12÷25%=48人.
社区服务的人数为48×50%=24,
补全折线统计如图所示:
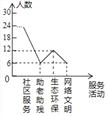
(2)网络文明部分对应的圆心角的度数为360°×![]() =45°;
=45°;
(3)分别用A,B,C,D表示“社区服务、助老助残、生态环保、网络文明”四个服务活动,
画树状图得:
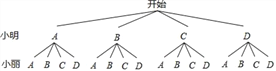
∵共有16种等可能的结果,他们参加同一服务活动的有4种情况,
∴他们参加同一服务活动的概率为![]() .
.