题目内容
【题目】用橡皮泥做一个棱长为4cm的正方体．
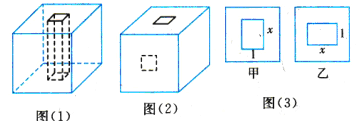
(1)如图(1)，在顶面中心位置处从上到下打一个边长为1cm的正方形通孔，打孔后的橡皮泥的表面积是多少？；
(2)如果在第(1)题打孔后，再在正面中心位置处(按图(2)中的虚线）从前到后打一个边长为1cm的正方形通孔，那么打孔后的橡皮泥的表面积为是多少？；
(3)如果把第(2)题中从前到后所打的正方形通孔扩大成一个长xcm、宽1cm的长方形通孔，能不能使所得橡皮泥的表面积为130cm2?如果能，请求出x；如果不能，请说明理由．
【答案】(1) 110；(2) 118；(3) x=3.
【解析】
（1）打孔后的表面积=原正方体的表面积-小正方形孔的面积+孔中的四个矩形的面积．
（2）打孔后的表面积=图（1）的表面积-4个小正方形孔的面积+新打的孔中的八个小矩形的面积
（3）分两种情形分别列出方程求解即可．
解：（1）表面积S1=96-2+4×4=110（cm2）；
故答案为110．
（2）表面积S2=S1-4+4×1.5×2=118（cm2）；
故答案为118．（3）能使橡皮泥块的表面积为130cm2，理由为：
①如图甲通孔，由题意，96-2-2（4-x）+3（2+2x）=130，
方程无解，不合题意．
②如图乙通孔，由题意，96-2-2x+4×3+4（2+2x）-2=130，
解得x=3，
∴当边长改为3cm时，表面积为130cm2．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
