题目内容
【题目】小明研究一函数的性质,下表是该函数的几组对应值:

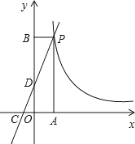
![]() 在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图像
![]() 根据所画函数图像,写出该函数的一条性质: .
根据所画函数图像,写出该函数的一条性质: .
![]() 根据图像直接写出该函数的解析式及自变量的取值范围: ;
根据图像直接写出该函数的解析式及自变量的取值范围: ;
![]() 若一次函数
若一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是 .
的范围是 .
【答案】(1)见解析;(2)![]() 时,
时,![]() 随
随![]() 的增大而减小;(3)
的增大而减小;(3)![]() (4)
(4)![]()
【解析】
![]() :根据表格中的格点,描点连线即可.
:根据表格中的格点,描点连线即可.
![]() 根据函数的图象写出函数的一条性质即可,例如
根据函数的图象写出函数的一条性质即可,例如![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
![]() 在
在![]() 时,函数是二次函数,当
时,函数是二次函数,当![]() 时,函数是一次函数,用待定系数法进行求解即可.
时,函数是一次函数,用待定系数法进行求解即可.
![]() 分两种情况,求出
分两种情况,求出![]() 的临界值,即可求出
的临界值,即可求出![]() 的范围.
的范围.
![]() 如图所示:
如图所示:
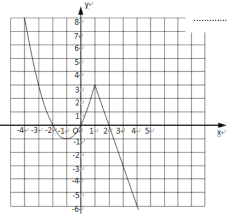
![]() 观察图象可知:
观察图象可知: ![]() 时,
时,![]() 随
随![]() 的增大而减小;(写出其他性质也可得分)
的增大而减小;(写出其他性质也可得分)
![]() 当
当![]() 时,设函数解析式为:
时,设函数解析式为:![]() 把点
把点![]() 代入得:
代入得:![]() 即
即![]()
![]()
当![]() 时,设函数解析式为:
时,设函数解析式为:![]() 把点
把点![]() 代入得:
代入得:![]() 解得
解得![]()
![]()
函数解析式为:![]()
![]() 一次函数
一次函数![]() 与该函数图像有三个交点,
与该函数图像有三个交点,
一次函数![]() 过点
过点![]() 时,一次函数
时,一次函数![]() 与该函数图像有两个交点,
与该函数图像有两个交点,
![]() 解得
解得![]()
联立方程: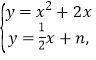 整理得:
整理得:![]()
![]() 时,
时,![]()
一次函数![]() 与该函数图像有两个交点,
与该函数图像有两个交点,
一次函数![]() 与该函数图像有三个交点,则
与该函数图像有三个交点,则![]() 的范围是:
的范围是:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知抛物线y=ax2+bx+3与y轴的交点为A,点A与点B关于抛物线的对称轴对称,二次函数y=ax2+bx+3的y与x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 8 | 0 | 0 | … |
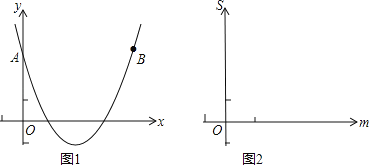
(1)抛物线的对称轴是 _________ .点A( ______, ____),B( _____, _____);
(2)求二次函数y=ax2+bx+3的解析式;
(3)已知点M(m,n)在抛物线y=ax2+bx+3上,设△BAM的面积为S,求S与m的函数关系式、画出函数图象.并利用函数图象说明S是否存在最大值,为什么?