��Ŀ����
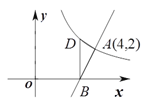
����Ŀ����֪������y=ax2+bx+3��y��Ľ���ΪA����A���B���������ߵĶԳ���Գƣ����κ���y=ax2+bx+3��y��x�IJ��ֶ�Ӧֵ���±���
x | �� | ��1 | 0 | 1 | 3 | 4 | �� |
y | �� | 8 | 0 | 0 | �� |
��1�������ߵĶԳ����� _________ ����A�� ______�� ____����B�� _____�� _____����
��2������κ���y=ax2+bx+3�Ľ���ʽ��
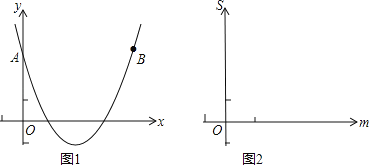
��3����֪��M��m��n����������y=ax2+bx+3�ϣ����BAM�����ΪS����S��m�ĺ�����ϵʽ����������ͼ�����ú���ͼ��˵��S�Ƿ�������ֵ��Ϊʲô��
���𰸡���1��x=2��A��0��3����B��4��3����
��2��y=x2-4x+3��
��3��S=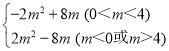 ��S���������ֵ����ͼ���֪����m��0��m��4ʱ��S��ֵ��������
��S���������ֵ����ͼ���֪����m��0��m��4ʱ��S��ֵ��������
��������
������1�����õ�x=1��3ʱ��y=0���ó������ߵĶԳ�����ֱ��x=2��������x=0ʱ��y=3�����A�� 0��3 �������ɵó�B�����ꣻ
��2������ͼ�����1��0������3��0������������Ϊy=a��x-1����x-3��������0��3������ɵó�a��ֵ�������ó�����ʽ��
��3����0��m��4ʱ����M��AB�ľ���Ϊ3-n����m��0��m��4ʱ����M��ֱ��AB�ľ���Ϊn-3����������������ó�S��m�ĺ�����ϵʽ������ͼ��ó�S�Ƿ�������ֵ��
�����������1�����ݵ�x=1��3ʱ��y=0���ó������ߵĶԳ����ǣ�ֱ��x=2��
��������y=ax2+bx+3��y��Ľ���ΪA��
��x=0ʱ��y=3�����A��0��3������B��4��3����
��2��ͼ�����1��0������3��0����
��������Ϊy=a��x-1����x-3����
����0��3������ɵã�3=a��0-1����0-3����
��ã�a=1��
�ʶ��κ���y=ax2+bx+3�Ľ���ʽΪ��y=��x-1����x-3��=x2-4x+3��
��3����ͼ1��
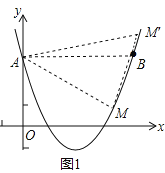
��AB��x�ᣬAB=4��
��0��m��4ʱ����M��AB�ľ���Ϊ3-n��
��S��ABM=![]() ��3-n����4=6-2n��
��3-n����4=6-2n��
����n=m2-4m+3��S1=-2m2+8m��
����m��0��m��4ʱ����M��ֱ��AB�ľ���Ϊn-3��S2=![]() ��4��n-3��=2n-6��
��4��n-3��=2n-6��
��n=m2-4m+3��S2=2m2-8m��
S=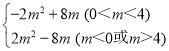 ��
��
�ʺ���ͼ����ͼ2��x���Ϸ���������ʾ��S���������ֵ����ͼ���֪����m��0��m��4ʱ��S��ֵ��������


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�