题目内容
一次函数y=x–3的图象与 轴,
轴, 轴分别交于点
轴分别交于点 .一个二次函数y=x2+bx+c的图象经过点
.一个二次函数y=x2+bx+c的图象经过点 .
.
(1)求点 的坐标,并画出一次函数y=x–3的图象;
的坐标,并画出一次函数y=x–3的图象;
(2)求二次函数的解析式并求其图像顶点C的坐标.
(3)求 的面积。
的面积。
(1)点A的坐标是(3,0),点B的坐标是(0,﹣3);
(2)二次函数的解析式是y=x2﹣2x﹣3,顶点C的坐标是(1,4);
(3)△ABC的面积是3.
解析试题分析:(1)分别把x=0、y=0代入求出y、x的值即可;
(2)把A、B的坐标代入二次函数的解析式得到方程组求出方程组的解即可,过A、B作直线即可;
(3)过C作CD⊥y轴于D,根据S△ABC=S梯形AODC﹣S△AOB﹣S△BDC,和数据线和梯形的面积公式求出即可.
试题解析:(1)y=x﹣3,当x=0时,y=﹣3,当y=0时,x=3,
∴A(3,0),B(0,﹣3).
直线y=k﹣3的图象如图所示: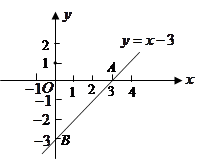
答:点A的坐标是(3,0),点B的坐标是(0,﹣3);
(2)把A(3,0),B(0,﹣3)代入次函数y=x2+bx+c得: ,
,
解得: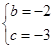 ,
,
∴y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴C的坐标是(1,﹣4),
答:二次函数的解析式是y=x2﹣2x﹣3,顶点C的坐标是(1,4);
(3)过C作CD⊥y轴于D,如图: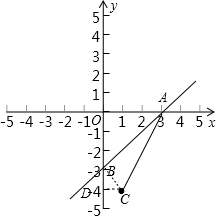
∵A(3,0),B(0,﹣3)C(1,﹣4),
∴OA=3,OB=3,CD=1,OD=4,BD=4﹣3=1,
∴S△ABC=S梯形AODC﹣S△AOB﹣S△BDC,
= ×(CD+OA)×OD﹣
×(CD+OA)×OD﹣ ×OA×OB﹣
×OA×OB﹣ ×DB×CD,
×DB×CD,
= ×(1+3)×4﹣
×(1+3)×4﹣ ×3×3﹣
×3×3﹣ ×1×1=3,
×1×1=3,
答:△ABC的面积是3.
考点:二次函数综合题.

练习册系列答案
相关题目
 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .
与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .

 与
与 轴和
轴和 的图象经过点A、B,且顶点为C.
的图象经过点A、B,且顶点为C.
 的值;
的值; ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标. (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE. 为定值;
为定值;

 ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元). %.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了
%.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了 %.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.
%.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.