Question

如图，已知抛物线y=ax²+bx﹣4与x轴交于A（﹣2，0），B（8，0）两点，与y轴交于点C，连接BC，以BC为一边，作菱形BDEC，使其对角线在坐标轴上，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．
（1）求抛物线的解析式；
（2）将抛物线向上平移n个单位，使其顶点在菱形BDEC内（不含菱形的边），求n的取值范围；
（3）当点P在线段OB上运动时，直线l交BD于点M．试探究m为何值时，四边形CQMD是平行四边形，并说明理由．

Answer 1

（1）y=x²﹣x﹣4；（2）；（3）m=4时，四边形CQMD是平行四边形，理由详见解析.

解析试题分析：（1）由待定系数法即可求得．
（2）先求得直线BC的解析式和抛物线的顶点坐标G（3，﹣），然后把x=3代入直线BC的解析式即可求得F的坐标，进而求得E的坐标即可求得n的取值．
（3）由菱形的对称性可知，点D的坐标，根据待定系数法可求直线BD的解析式，根据平行四边形的性质可得关于m的方程，求得m的值；再根据平行四边形的判定可得四边形CQBM的形状；
试题解析:（1）∵抛物线y=ax²+bx﹣4与x轴交于A（﹣2，0），B（8，0）两点，
∴ 解得
∴抛物线的解析式为：y=x²﹣x﹣4；
（2）设抛物线的顶点为G，过G点作x轴的垂线交BD于E，交BC于F，
由抛物线的解析式y=x²﹣x﹣4可知C（0，﹣4）
设直线BC的解析式为y=k₁x+b₁，
∵B（8，0），C（0，﹣4），则，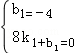
解得k₁=，b₁=﹣4．
故直线BC的解析式为y=x﹣4．
∵y=x²﹣x﹣4=（x﹣3）²﹣，
∴抛物线的顶点G的坐标（3，﹣），
当x=3时，y=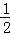x﹣4=﹣，
∴F（3，﹣），
由菱形的对称性可知，点E的坐标为（3，）．
∵GF=﹣﹣（﹣）=，GE=﹣（﹣）=，
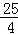∴＜n＜．
（3）∵C（0，﹣4）
∴由菱形的对称性可知，点D的坐标为（0，4）．
设直线BD的解析式为y=kx+b，则，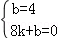
解得k=﹣，b=4．
∴直线BD的解析式为y=﹣x+4．
∵l⊥x轴，
∴点M的坐标为（m，﹣m+4），点Q的坐标为（m，m²﹣m﹣4）．
如图，当MQ=DC时，四边形CQMD是平行四边形，
∴（﹣m+4）﹣（ m²﹣m﹣4）=4﹣（﹣4）．
化简得：m²﹣4m=0，
解得m₁=0（不合题意舍去），m₂=4．
∴当m=4时，四边形CQMD是平行四边形．

考点：1.待定系数法求函数解析式；2.平行四边形判定