题目内容
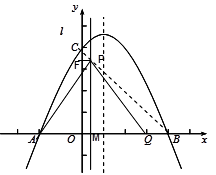
如图,抛物线:y=ax2+bx+4与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ACT是以AC为底的等腰三角形,求点T的坐标;
(3)点M、Q分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行.当点M原点时,点Q立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动.过点M的直线l⊥轴,交AC或BC于点P.求点M的运动时间t(秒)与△APQ的面积S的函数关系式,并求出S的最大值.
(1)抛物线的解析式为: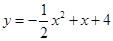 ;
;
(2)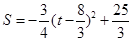 ,S的最大值为
,S的最大值为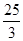 .
.
解析试题分析:(1)把A、B的坐标代入抛物线的解析式得到方程组,求出方程组的解即可;
(2)设直线x=1上一点T(1,h),连接TC、TA,作CE⊥直线x=1,垂足是E,根据TA=TC由勾股定理求出即可;
(3)(I)当0<t≤2时,△AMP∽△AOC,推出比例式,求出PM,AQ,根据三角形的面积公式求出即可;
(II)当2<t≤3时,作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APQ的面积,利用配方法求出最值即可.
试题解析:(1)把A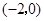 、B(4,0)代入
、B(4,0)代入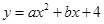 ,得
,得
解得
∴抛物线的解析式为: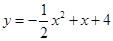 ;
;
(2)由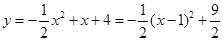 ,得抛物线的对称轴为直线
,得抛物线的对称轴为直线 ,
,
直线 交x轴于点D,设直线
交x轴于点D,设直线 上一点T(1,h),连结TC,TA,作CE⊥直线
上一点T(1,h),连结TC,TA,作CE⊥直线 ,垂足为E,由C(0,4)得点E(1,4),
,垂足为E,由C(0,4)得点E(1,4),
在Rt△ADT和Rt△TEC中,由TA=TC得
解得 ,
,
∴点T的坐标为(1,1);
(3)解:(Ⅰ)当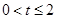 时,△AMP∽△AOC
时,△AMP∽△AOC
∴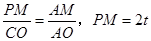
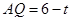
∴
当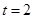 时,S的最大值为8.
时,S的最大值为8.
(Ⅱ)当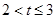 时,
时,
作PF⊥y轴于F,有△COB∽△CFP,又CO=OB
∴FP=FC=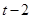 ,
,
∴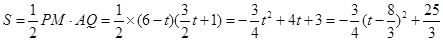
∴当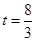 时,则S的最大值为
时,则S的最大值为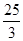 ,
,
综合Ⅰ、Ⅱ,S的最大值为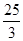 .
.
考点:二次函数综合题.

今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=-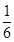 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
(1)求出z与x的函数关系式;
(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?
 与
与 轴的交点的个数是___________.
轴的交点的个数是___________.
 的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4. .
.
 轴,
轴, 轴分别交于点
轴分别交于点 .一个二次函数y=x2+bx+c的图象经过点
.一个二次函数y=x2+bx+c的图象经过点 的面积。
的面积。

 ;
;