题目内容
为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本(元)与月份之间的关系可近似地表示为: ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).
(1)分别求出y与x,w与x的函数关系式;
(2)在今年内该单位哪个月获得利润达到5800元?
(3)随着人们环保意识的增加,该单位需求的可再生资源数量受限.今年三月的再生资源处理量比二月份减少了m%,该新产品的产量也随之减少,其售价比二月份的售价增加了 %.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了
%.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了 %.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.
%.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.
(1) y=10x+30,w=-50x2+900x+2550;(2)5;(3)10.
解析试题分析:(1)首先根据表格求出y与x的函数关系式,然后利用已知条件即可得到P与x的函数关系式;
(2)根据(1)所求可以进而得到利润与x之间的函数关系式,即可求解;
(3)首先根据已知条件可以分别求出:二月处理量、二月成本、二月利润,接着利用已知条件即可列出方程100×50(1-m%)(1+0.6m%)-850×(1-20%)=50×100-850-60,解方程即可解决问题.
试题解析::解:(1)将(1,40),(2,50)代入y=kx+b,
得: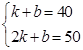 ,解得:
,解得: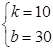
故每月再生资源处理量y(吨)与x月份之间的关系式为:y=10x+30,
w=100y-p
=100(10x+30)-(50x2+100x+450)
=-50x2+900x+2550
(2)由-50x2+900x+2550=5800得:
x2-18x+65=0
∴x1=13,x2=5
∵x≤12,
∴x=5
∴在今年内该单位第5个月获得利润达到5800元.
(3)二月份再生资源处理量:40+10=50吨,
二月成本:P=50×22+100×2+450=850元,
100×50(1-m%)(1+0.6m%)-950×(1-20%)=4050,
令m%=t,则300t2+200t-23=0
∴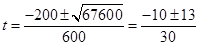
∵t>0
∴t=0.1
∴m%=0.1,即m=10.
考点:二次函数的应用.

 阅读快车系列答案
阅读快车系列答案今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=-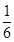 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
(1)求出z与x的函数关系式;
(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?
 ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
 轴,
轴, 轴分别交于点
轴分别交于点 .一个二次函数y=x2+bx+c的图象经过点
.一个二次函数y=x2+bx+c的图象经过点 的面积。
的面积。

 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.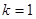 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标; 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 与
与 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围; 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
