��Ŀ����
��ͼ��������ABCD�ı߳���3����P��ֱ��BC��һ�㣬����PA�����߶�PA�Ƶ�P��ʱ����ת90��õ��߶�PE����ֱ��BA��ȡ��F��ʹBF=BP���ҵ�F���E��BCͬ�࣬����EF��CF��

��1����ͼ�٣�����P��CB�ӳ�����ʱ����֤���ı���PCFE��ƽ���ı��Σ�
��2����ͼ�ڣ�����P���߶�BC��ʱ���ı���PCFE�Ƿ���ƽ���ı��Σ�˵�����ɣ�
��3���ڣ�2���������£��ı���PCFE������Ƿ������ֵ�����У��������������ֵ����ʱBP������û�У���˵�����ɣ�

��1����ͼ�٣�����P��CB�ӳ�����ʱ����֤���ı���PCFE��ƽ���ı��Σ�
��2����ͼ�ڣ�����P���߶�BC��ʱ���ı���PCFE�Ƿ���ƽ���ı��Σ�˵�����ɣ�
��3���ڣ�2���������£��ı���PCFE������Ƿ������ֵ�����У��������������ֵ����ʱBP������û�У���˵�����ɣ�
�⣺��1�����ı���ABCD�������Σ���AB=BC����ABC=��PBA=90��
���ڡ�PBA�͡�FBC�У�AB=BC����PBA=��FBC��BP=BF��
���PBA�ա�FBC��SAS������PA=FC����PAB=��FCB��
��PA=PE����PE=FC��
�ߡ�PAB+��APB=90�㣬���FCB+��APB=90�㡣
�ߡ�EPA=90�㣬���APB+��EPA+��FPC=180�㣬����EPC+��PCF=180�㡣
��EP��FC�����ı���EPCF��ƽ���ı��Ρ�
��2�����ۣ��ı���EPCF��ƽ���ı��Σ��������£�
���ı���ABCD�������Σ���AB=BC����ABC=��CBF=90�㡣
���ڡ�PBA�͡�FCB�У�AB=BC����PBA=��FBC��BP=BF��
���PBA�ա�FBC��SAS������PA=FC����PAB=��FCB��
��PA=PE����PE=FC��
�ߡ�FCB+��BFC=90�㣬��EPB+��APB=90�㣬���BPE=��FCB��
��EP��FC�����ı���EPCF��ƽ���ı��Ρ�
��3����
��BP=x����PC=3��x ��ƽ���ı���PEFC�����ΪS��
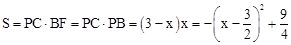 ��
��
��a=��1��0���������ߵĿ������£�
�൱x=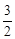 ʱ��S���=
ʱ��S���=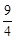 ��
��
�൱BP=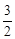 ʱ���ı���PCFE�����������ֵΪ
ʱ���ı���PCFE�����������ֵΪ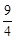 ��
��
���ڡ�PBA�͡�FBC�У�AB=BC����PBA=��FBC��BP=BF��
���PBA�ա�FBC��SAS������PA=FC����PAB=��FCB��
��PA=PE����PE=FC��
�ߡ�PAB+��APB=90�㣬���FCB+��APB=90�㡣
�ߡ�EPA=90�㣬���APB+��EPA+��FPC=180�㣬����EPC+��PCF=180�㡣
��EP��FC�����ı���EPCF��ƽ���ı��Ρ�
��2�����ۣ��ı���EPCF��ƽ���ı��Σ��������£�
���ı���ABCD�������Σ���AB=BC����ABC=��CBF=90�㡣
���ڡ�PBA�͡�FCB�У�AB=BC����PBA=��FBC��BP=BF��
���PBA�ա�FBC��SAS������PA=FC����PAB=��FCB��
��PA=PE����PE=FC��
�ߡ�FCB+��BFC=90�㣬��EPB+��APB=90�㣬���BPE=��FCB��
��EP��FC�����ı���EPCF��ƽ���ı��Ρ�
��3����
��BP=x����PC=3��x ��ƽ���ı���PEFC�����ΪS��
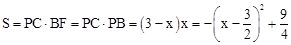 ��
����a=��1��0���������ߵĿ������£�
�൱x=
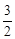 ʱ��S���=
ʱ��S���=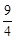 ��
���൱BP=
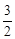 ʱ���ı���PCFE�����������ֵΪ
ʱ���ı���PCFE�����������ֵΪ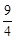 ��
�������������1���������ε����ʿ��Եó�AB=BC����ABP=��ABC=��90�㣬���Եó���PBA�ա�FBC���������ʾͿ��Եó����ۡ�
��2���������ε����ʿ��Եó�AB=BC����FBC=��ABC=��90�㣬���Եó���PBA�ա�FBC���������ʾͿ��Եó����ۡ�
��3����BP=x����PC=3��x ƽ���ı���PEFC�����ΪS����ƽ���ı��ε������ʽ�Ϳ�����������ʽ���ٸ��ݶ��κ��������ʾͿ�����������ֵ����

��ϰ��ϵ�д�
�����Ŀ







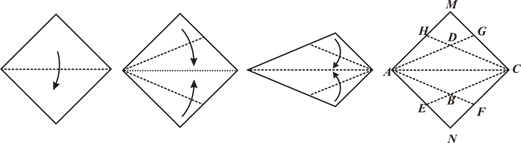

 ����AB�ij���
����AB�ij���

