题目内容
如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC= ,求AB的长。
,求AB的长。

(1)求证:OE=OF;
(2)若BC=
 ,求AB的长。
,求AB的长。解:(1)证明:∵四边形ABCD是矩形,∴DC∥AB。
∴∠OAE=∠OCF,∠OEA=∠OFC。
又∵AE=CF,∴△OEA≌△OFC(ASA)。
∴OE=OF。
(2)如图,连接OB,
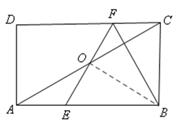
∵BE=BF,OE=OF,∴BO⊥EF,∠ABO=∠OBF。
∵∠BEF=2∠BAC,∴∠OBE=∠BAC。
又∵矩形ABCD中,∠ABC=900,∴∠BOE=∠ABC=900。
∴△OBE∽△BAC。∴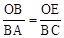 。
。
∵∠BEF=2∠BAC,∴∠OAE=∠AOE。∴AE=OE。
设AB=x,AE=OE=y,则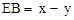 。
。
∵BC= ,∴
,∴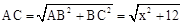 。
。
由(1)△OEA≌△OFC,得AO=CO,∴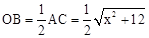 。
。
∴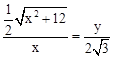 。∴
。∴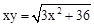 ①。
①。
又∵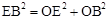 ,即
,即 ,
,
化简,得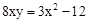 ②。
②。
由①②得 ,两边平方并化简,得
,两边平方并化简,得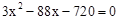 ,
,
∴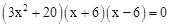 ,∴根据x的实际意义,得x=6。
,∴根据x的实际意义,得x=6。
∴若BC= , AB的长为6。
, AB的长为6。
∴∠OAE=∠OCF,∠OEA=∠OFC。
又∵AE=CF,∴△OEA≌△OFC(ASA)。
∴OE=OF。
(2)如图,连接OB,

∵BE=BF,OE=OF,∴BO⊥EF,∠ABO=∠OBF。
∵∠BEF=2∠BAC,∴∠OBE=∠BAC。
又∵矩形ABCD中,∠ABC=900,∴∠BOE=∠ABC=900。
∴△OBE∽△BAC。∴
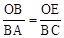 。
。∵∠BEF=2∠BAC,∴∠OAE=∠AOE。∴AE=OE。
设AB=x,AE=OE=y,则
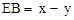 。
。∵BC=
 ,∴
,∴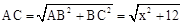 。
。由(1)△OEA≌△OFC,得AO=CO,∴
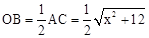 。
。∴
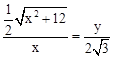 。∴
。∴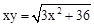 ①。
①。又∵
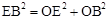 ,即
,即 ,
,化简,得
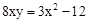 ②。
②。由①②得
 ,两边平方并化简,得
,两边平方并化简,得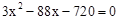 ,
,∴
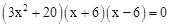 ,∴根据x的实际意义,得x=6。
,∴根据x的实际意义,得x=6。∴若BC=
 , AB的长为6。
, AB的长为6。(1)由矩形的性质,结合已知可根据ASA证出△OEA≌△OFC,从而得出结论
(2)连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,∠ABO=∠OBF,从而得到△OBE∽△BAC,设出未知数和参数:AB=x,AE=OE=y,可得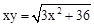 ,在Rt△OBE中应用勾股定理得
,在Rt△OBE中应用勾股定理得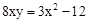 ,二者联立,解出x即可。
,二者联立,解出x即可。
(2)连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,∠ABO=∠OBF,从而得到△OBE∽△BAC,设出未知数和参数:AB=x,AE=OE=y,可得
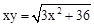 ,在Rt△OBE中应用勾股定理得
,在Rt△OBE中应用勾股定理得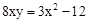 ,二者联立,解出x即可。
,二者联立,解出x即可。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 cm
cm
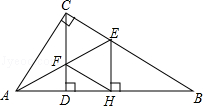
 等于【 】
等于【 】
 B.
B. C.
C. D.
D.