题目内容
【题目】已知二次函数y=x2﹣2x﹣3．
（1）将y=x2﹣2x﹣3化成y=a（x﹣h）2+k的形式；
（2）与y轴的交点坐标是 ， 与x轴的交点坐标是；
（3）在坐标系中利用描点法画出此抛物线．
x | … | … | |||||
y | … | … |
（4）不等式x2﹣2x﹣3＞0的解集是 ． 
【答案】
（1）解：y=x2﹣2x﹣3=x2﹣2x+1﹣3﹣1=（x﹣1）2﹣4，即y=（x﹣1）2﹣4
（2）（0，﹣3）；（3，0）（﹣1，0）
（3）解：列表：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
图象如图所示：
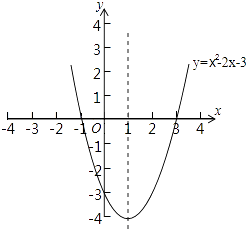
（4）x＜﹣1或x＞3
【解析】解：（2）令x=0，则y=﹣3，即该抛物线与y轴的交点坐标是 （0，﹣3），
又y=x2﹣2x﹣3=（x﹣3）（x+1），
所以该抛物线与x轴的交点坐标是（3，0）（﹣1，0）．
故答案是：（0，﹣3）；（3，0）（﹣1，0）；（4）如图所示，不等式x2﹣2x﹣3＞0的解集是x＜﹣1或x＞3．
故答案是：x＜﹣1或x＞3．
【考点精析】本题主要考查了二次函数的图象的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
