题目内容
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示．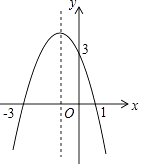 
（1）求这个二次函数的解析式；
（2）根据图象，写出当x取何值时，y＞0？
【答案】
（1）解：∵图象过（﹣3，0），（1，0），
∴设抛物线的解析式为y=a（x+3）（x﹣1）（a≠0），
∵图象过（0，3），
∴3=a（0+3）（0﹣1），
a=﹣1，
∴y=﹣（x+3）（x﹣1），
即y=﹣x2﹣2x+3
（2）解：由图象可知，当﹣3＜x＜1，y＞0
【解析】（1）设抛物线的解析式为y=a（x+3）（x﹣1）（a≠0），图象过点（0，3），求出a的值，即可求出二次函数的解析式；（2）直接根据图象写出x的取值范围．
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．才能正确解答此题．
【题目】某中学开展“八荣八耻”演讲比赛活动，九
、九
班根据初赛成绩各选出
名选手参加复赛，两个班各选出的名选手的复赛成绩（满分为
分）如下图所示：
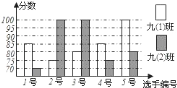
（1）根据上图填写下表：
平均分（分） | 中位数（分） | 众数（分） | |
九 |
|
| |
九 |
|
|
结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好？
（3）如果在每班参加复赛的选手中分别选出
人参加决赛，你认为哪个班的实力更强一些，说明理由．
【题目】已知二次函数y=x2﹣2x﹣3．
（1）将y=x2﹣2x﹣3化成y=a（x﹣h）2+k的形式；
（2）与y轴的交点坐标是 ， 与x轴的交点坐标是；
（3）在坐标系中利用描点法画出此抛物线．
x | … | … | |||||
y | … | … |
（4）不等式x2﹣2x﹣3＞0的解集是 ． 
