题目内容
【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C. 
(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标.
【答案】
(1)解:当x=0时,y=﹣5,
当y=0时,5x﹣5=0,
解得,x=1,
则点A的坐标为(1,0),点B的坐标为(0,﹣5),
则点C的坐标(0,5)
(2)解:由题意得, 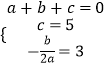 ,
,
解得,a=1,b=﹣6,c=5,
则抛物线的解析式为y=x2﹣6x+5
(3)解:设点P的坐标为(x,0),
y=x2﹣6x+5=(x﹣3)2﹣4,
则点D的坐标为(3,﹣4),
由题意得, ![]() ×|x﹣1|×4=6,
×|x﹣1|×4=6,
解得,x=﹣2或4,
则点P的坐标为(﹣2,0)或(4,0)
【解析】(1)根据一次函数图象上点的坐标特征求出点A和点B的坐标,根据中心对称的性质求出点C的坐标;(2)利用待定系数法求出抛物线y=ax2+bx+c的解析式;(3)利用二次函数的性质求出点D的坐标,根据三角形的面积公式计算即可.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.

【题目】已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 , 与x轴的交点坐标是;
(3)在坐标系中利用描点法画出此抛物线.
x | … | … | |||||
y | … | … |
(4)不等式x2﹣2x﹣3>0的解集是 .