题目内容
【题目】如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E. 
(1)求证:AC∥DE;
(2)若OA=AE=4,求AC的长.
【答案】
(1)证明:∵OD过圆心,F为AC中点,
∴OD⊥AC,
∵ED切⊙O于D,
∴OD⊥ED,
∴AC∥DE
(2)解:∵OD=OA=4,OE=OA+AE=8,
∴OD= ![]() OE,
OE,
∵在Rt△ODE中,OD= ![]() OE,
OE,
∴∠E=30°,
∵AC∥DE,
∴∠CAB=∠E=30°,
∴在Rt△OAF中,OF= ![]() AO=2,AF=
AO=2,AF= ![]() OF=2
OF=2 ![]() ,
,
∵F为AC中点,
∴AC=2AF=4 ![]()
【解析】(1)由点F为弦AC的中点,ED切⊙O于D,可得OD⊥AC,OD⊥DE,继而证得结论;(2)由OA=AE=4,易得∠E=30°,又由AC∥DE,利用三角函数的知识即可求得OF,AF的长,继而求得答案.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

【题目】未成年人思想道德建设越来越受到社会的关注,辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成了频
分组 | 频数 | 频率 |
0.5~50.5 |
| 0.1 |
50.5~ | 20 | 0.2 |
100.5~150.5 |
|
|
200.5 | 30 | 0.3 |
200.5~250.5 | 10 | 0.1 |
率分布表和频率分布直方图(如图).
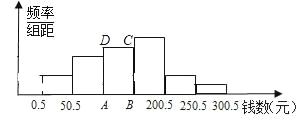
(1)补全频率分布表;
(2)在频率分布直方图中,长方形ABCD的面积是 ;这次调查的样本容量是 ;
(3)研究所认为,应对消费150元以上的学生提出勤俭节约的建议.试估计应对该校1000名学生中约多少名学生提出这项建议.
【题目】已知二次函数y=x2﹣2x﹣3.
(1)将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)与y轴的交点坐标是 , 与x轴的交点坐标是;
(3)在坐标系中利用描点法画出此抛物线.
x | … | … | |||||
y | … | … |
(4)不等式x2﹣2x﹣3>0的解集是 .