Question

一块三角形布料，三边长分别为13，14，15，需要裁出一圆形布料，其半径的最大值为（　　）

A．4

B．6.5

C．7

D．7.5

Answer 1

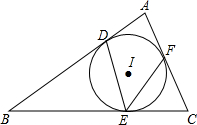
如图，AB=13，AC=14，BC=15，⊙O为△ABC的内切圆，切点分别为D、E、F，AH为BC边上的高，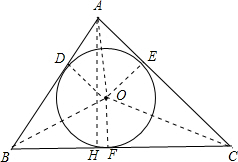
设⊙O的半径为R，BH=x，AH=h，则HC=15-x，OD=OE=OF=R，
在Rt△ABH中，AH²+BH²=AB²，即h²+x²=13²①，
在Rt△ACH中，AH²+CH²=AB²，即h²+（15-x）²=14²②，
②-①得225-30x=196-169，
解得x=

33

5

，
把x=

33

5

代入①得h²+（

33

5

）²=13²，
解得h=

56

5

，
∵S_△ABC=S_△OAB+S_△AOC+S_△OBC，
∴

1

2

h•BC=

1

2

AB•R+

1

2

AC•R+

1

2

BC•R，
∴（13+14+15）•R=

56

5

×15，
解得R=4．
即圆形布料的半径的最大值为4．
故选A．