题目内容
如图,点M(m,n)在第一象限,且2
+3
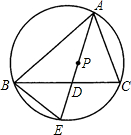
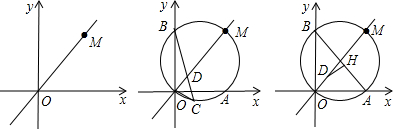
=n-4,过O、M两点作圆分别与x轴正半轴,y轴正半轴交于A、B两点,C在弧AO上,BC交OM于D,且CO=CD.
(1)求M点的坐标;
(2)若∠BDM=60°,连AM,求
的值;
(3)过D作DH⊥AB于H,下列结论:①DH+
AB的值不变;②DH+AB的值不变,其中有且只有一个结论是正确的,请你作出正确判断并予以证明.
| m-4 |
| 8-2m |
(1)求M点的坐标;
(2)若∠BDM=60°,连AM,求
| AM |
| OB |
(3)过D作DH⊥AB于H,下列结论:①DH+
| 1 |
| 2 |

(1)∵2
+3
=n-4,
∴
解得,m=4,
∴n=4,
∴M点的坐标(4,4);
(2)∵AB是直径,∠BOM=∠MOA=45°,
∴等腰Rt△MAB,AM=
AB,
∵∠BDM=60°,
∴∠ODC=60°,
∵CO=CD,
∴△OCD是等边三角形,
∴∠BAO=∠BMO=60°,
∵∠BDM=60°,
∴△DBM是等边三角形,
∴OB=
AB,
∴
=
=
;
(3)由图可知:
∵CO=CD,∠ODC=∠D0C,
∴∠ODC=45°+∠OBC,∠D0C=45°+∠AOC=45°+∠ABC,
∴∠OBC=∠ABC,D为△BOA内心,
过点D作DF⊥OA于点F,DE⊥BO于点E,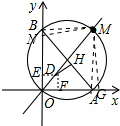
∴DH=DE=DF,BH=BE,AH=AF,
∠DEO=∠EOF=∠OFD=90°,
∴四边形EOFD是正方形,
∴BE+AF=BH+AF=AB,
∴OA+OB=OE+BE+OF+AF=DH+BE+DH+AF=2HD+AB,
过点M做MG⊥x轴,MN⊥y轴,垂足分别为G,N,
则MG=MN=4,
∴ON=OG=4,
又∵∠BAM=∠BOM=45°,
∠ABM=∠MOA=45°,
∴∠ABM=∠BAM,
∴MB=MA,
∴△BMN≌△AMG,
∴BN=AG,
∴OB+OA=ON+BN+OA=ON+AG+OA=ON+OG=4+4=8,
∴2HD+AB=8,
∴HD+
AB=4,
故①DH+
AB的值不变.
| m-4 |
| 8-2m |
∴
|
解得,m=4,
∴n=4,
∴M点的坐标(4,4);
(2)∵AB是直径,∠BOM=∠MOA=45°,
∴等腰Rt△MAB,AM=
| ||
| 2 |
∵∠BDM=60°,
∴∠ODC=60°,
∵CO=CD,
∴△OCD是等边三角形,
∴∠BAO=∠BMO=60°,
∵∠BDM=60°,
∴△DBM是等边三角形,
∴OB=
| ||
| 2 |
∴
| AM |
| OB |
| ||
|
| ||
| 3 |
(3)由图可知:
∵CO=CD,∠ODC=∠D0C,
∴∠ODC=45°+∠OBC,∠D0C=45°+∠AOC=45°+∠ABC,
∴∠OBC=∠ABC,D为△BOA内心,
过点D作DF⊥OA于点F,DE⊥BO于点E,

∴DH=DE=DF,BH=BE,AH=AF,
∠DEO=∠EOF=∠OFD=90°,
∴四边形EOFD是正方形,
∴BE+AF=BH+AF=AB,
∴OA+OB=OE+BE+OF+AF=DH+BE+DH+AF=2HD+AB,
过点M做MG⊥x轴,MN⊥y轴,垂足分别为G,N,
则MG=MN=4,
∴ON=OG=4,
又∵∠BAM=∠BOM=45°,
∠ABM=∠MOA=45°,
∴∠ABM=∠BAM,
∴MB=MA,
∴△BMN≌△AMG,
∴BN=AG,
∴OB+OA=ON+BN+OA=ON+AG+OA=ON+OG=4+4=8,
∴2HD+AB=8,
∴HD+
| 1 |
| 2 |
故①DH+
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目