题目内容
【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
【答案】(1)![]() .(2)当售价为175元时,月销售利润最大,最大利润是11250元.(3)
.(2)当售价为175元时,月销售利润最大,最大利润是11250元.(3)![]() .
.
【解析】
(1)将点![]() 、
、![]() 代入一次函数表达式:
代入一次函数表达式:![]() 即可求解;
即可求解;
(2)设运动服的进价为![]() 元,则月销售利润
元,则月销售利润![]() ,即可求解;
,即可求解;
(3)由题意得:![]() ,函数的对称轴为:
,函数的对称轴为:![]() ,
,![]() ,假设函数在对称轴处取得最大值,在
,假设函数在对称轴处取得最大值,在![]() ,则
,则![]() ,不合题意,则函数在
,不合题意,则函数在![]() 处取得最大值,将
处取得最大值,将![]() 代入函数表达式,即可求解.
代入函数表达式,即可求解.
(1)解:设y关于x的函数解析式为:![]()
把点(120,260),(160,180)代入一次函数表达式![]() 得:
得:
![]() 解得:
解得:![]()
则函数的表达式为:![]() .
.
(2)设运动服的进价为a元,则月销售利润为:![]()
由表格第一列知:![]() ,解得
,解得![]() .
.
![]()
∵![]()
∴w有最大值,当![]() 时,w的最大值为11250.
时,w的最大值为11250.
(3)由题意得:![]() .
.
函数的对称轴为:![]()
由于![]()
假设函数在对称轴处取得最大值,在![]() ,则
,则![]() ,不合题意舍去
,不合题意舍去
则函数在![]() 处取得最大值,将
处取得最大值,将![]() 代入函数表达式得:
代入函数表达式得:
![]()
解得:![]() .
.

【题目】某服装公司有![]() 型童装80件,
型童装80件,![]() 型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
型童装120件,分配给下属的“万达”和“万象城”两个专卖店销售,其中140件给万达店,60件给万象城店,且都能卖完,两商店销售这两种童装每件的利润(元)如表:
|
| |
万达店 | 100 | 80 |
万象城店 | 80 | 90 |
(1)设分配给万达店![]() 型产品
型产品![]() 件(
件(![]() ),请在下表中用含
),请在下表中用含![]() 的代数式填写:
的代数式填写:
|
| |
万达店 |
| ______ |
万象城店 | ______ | ______ |
若记这家服装公司卖出这200件产品的总利润为![]() (元),求
(元),求![]() 关于
关于![]() 的函数关系.
的函数关系.
(2)现要求总利润不低于18140元,请说明有多少种不同分配方案,并写出各种分配方案.
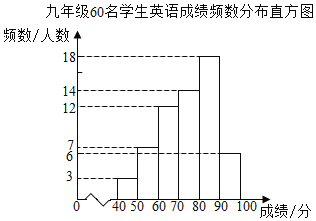
【题目】在新冠病毒疫情防控期间,某校“停课不停学”,开展了网络教学.为了解九年级学生在网络学习期间英语学科和数学学科的学习情况,复课后从九年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制)的数据,通过对成绩数据的整理、描述和分析,得到了如下部分信息.
①英语成绩的频数分布直方图如图:
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100.)
②英语和数学成绩的平均数、中位数、众数如表:
学科 | 平均数 | 中位数 | 众数 |
英语 | 74.8 | m | 83 |
数学 | 72.2 | 70 | 81 |
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值是 .
(2)在此次测试中,李丽的英语成绩为74分,数学成绩为71分,该名学生成绩排名更靠前的学科是 .(填“英语”或“数学”),理由是 .
(3)若该校九年级共有500名学生,请你估计英语成绩超过77.5分的人数.