ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥Јю„∞єЂЋЊ”–![]() –ЌЌѓ„∞80Љю£ђ
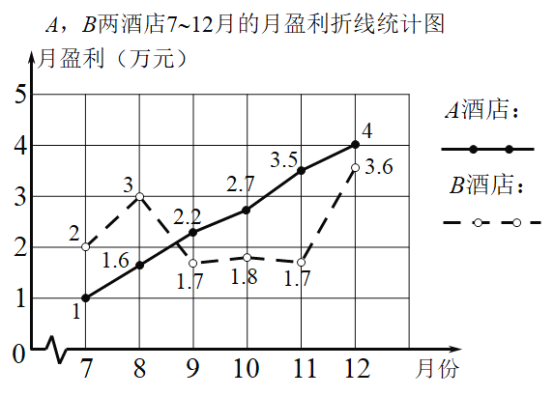
–ЌЌѓ„∞80Љю£ђ![]() –ЌЌѓ„∞120Љю£ђЈ÷≈дЄшѕ¬ фµƒ°∞Ќтіп°±ЇЌ°∞Ќтѕу≥«°±ЅљЄц„®¬фµкѕъ џ£ђ∆д÷–140ЉюЄшЌтіпµк£ђ60ЉюЄшЌтѕу≥«µк£ђ«“ґЉƒ№¬фЌк£ђЅљ…ћµкѕъ џ’вЅљ÷÷Ќѓ„∞√њЉюµƒјы»у£®‘™£©»з±н£Ї
–ЌЌѓ„∞120Љю£ђЈ÷≈дЄшѕ¬ фµƒ°∞Ќтіп°±ЇЌ°∞Ќтѕу≥«°±ЅљЄц„®¬фµкѕъ џ£ђ∆д÷–140ЉюЄшЌтіпµк£ђ60ЉюЄшЌтѕу≥«µк£ђ«“ґЉƒ№¬фЌк£ђЅљ…ћµкѕъ џ’вЅљ÷÷Ќѓ„∞√њЉюµƒјы»у£®‘™£©»з±н£Ї
|
| |
Ќтіпµк | 100 | 80 |
Ќтѕу≥«µк | 80 | 90 |
£®1£©…иЈ÷≈дЄшЌтіпµк![]() –Ќ≤ъ∆Ј
–Ќ≤ъ∆Ј![]() Љю£®
Љю£®![]() £©£ђ«л‘Џѕ¬±н÷–”√Їђ
£©£ђ«л‘Џѕ¬±н÷–”√Їђ![]() µƒіъ э љћо–і£Ї
µƒіъ э љћо–і£Ї
|
| |
Ќтіпµк |
| ______ |
Ќтѕу≥«µк | ______ | ______ |
»фЉ«’вЉ“Јю„∞єЂЋЊ¬ф≥ц’в200Љю≤ъ∆Јµƒ„№јы»уќ™![]() £®‘™£©£ђ«у
£®‘™£©£ђ«у![]() єЎ”Џ
єЎ”Џ![]() µƒЇѓ эєЎѕµ£Ѓ
µƒЇѓ эєЎѕµ£Ѓ
£®2£©ѕ÷“™«у„№јы»у≤їµЌ”Џ18140‘™£ђ«лЋµ√ч”–ґа…ў÷÷≤їЌђЈ÷≈дЈљ∞Є£ђ≤Ґ–і≥цЄч÷÷Ј÷≈дЈљ∞Є£Ѓ
°Њір∞Є°њ£®1£©ћо±нЉыѕкљв£ђ![]() £ї
£ї
£®2£©Ј÷≈дЈљ∞Є”–»э÷÷£Ї
Јљ∞Є“ї£ЇЄшЌтіпµк![]() –Ќ≤ъ∆Ј78Љю£ђ
–Ќ≤ъ∆Ј78Љю£ђ![]() –Ќ≤ъ∆Ј62Љю£ђЄшЌтѕу≥«µк
–Ќ≤ъ∆Ј62Љю£ђЄшЌтѕу≥«µк![]() –Ќ≤ъ∆Ј2Љю£ђ
–Ќ≤ъ∆Ј2Љю£ђ![]() –Ќ≤ъ∆Ј58Љю£ї
–Ќ≤ъ∆Ј58Љю£ї
Јљ∞Єґю£ЇЄшЌтіпµк![]() –Ќ≤ъ∆Ј79Љю£ђ
–Ќ≤ъ∆Ј79Љю£ђ![]() –Ќ≤ъ∆Ј61Љю£ђЄшЌтѕу≥«µк
–Ќ≤ъ∆Ј61Љю£ђЄшЌтѕу≥«µк![]() –Ќ≤ъ∆Ј1Љю£ђ
–Ќ≤ъ∆Ј1Љю£ђ![]() –Ќ≤ъ∆Ј59Љю£ї
–Ќ≤ъ∆Ј59Љю£ї
Јљ∞Є»э£ЇЄшЌтіпµк![]() –Ќ≤ъ∆Ј80Љю£ђ
–Ќ≤ъ∆Ј80Љю£ђ![]() –Ќ≤ъ∆Ј60Љю£ђЄшЌтѕу≥«µк
–Ќ≤ъ∆Ј60Љю£ђЄшЌтѕу≥«µк![]() –Ќ≤ъ∆Ј0Љю£ђ
–Ќ≤ъ∆Ј0Љю£ђ![]() –Ќ≤ъ∆Ј60Љю£Ѓ
–Ќ≤ъ∆Ј60Љю£Ѓ
°Њљвќц°њ
£®1£©ЄщЊЁЌтіпµкє≤–и140Љю£ђ“—Њ≠”–![]() –ЌxЉю£ђЋщ“‘–и“™B–Ќ£®140-x£©Љю£ђA–Ќ“їє≤80Љю£ђЋщ“‘Ќтѕу≥«µк–и“™Ј÷≈дA–Ќ£®80-x£©Љю£ђ–и“™Ј÷≈дB–Ќ[120-£®140-x£©]=£®x-20£©Љю£їЄщЊЁ°∞„№јы»у=ЌтіпµкABЅљ÷÷–ЌЇ≈јы»уЇЌ+Ќтѕу≥«µкABЅљ÷÷–ЌЇ≈јы»у°±Љіњ…Ѕ–≥цЇѓ эєЎѕµ љ£ђ≤ҐЄщЊЁ±нЄсЄчЅњ µЉ “в“ењ…“‘»Јґ®„‘±дЅњ»°÷µЈґќІ£ї
–ЌxЉю£ђЋщ“‘–и“™B–Ќ£®140-x£©Љю£ђA–Ќ“їє≤80Љю£ђЋщ“‘Ќтѕу≥«µк–и“™Ј÷≈дA–Ќ£®80-x£©Љю£ђ–и“™Ј÷≈дB–Ќ[120-£®140-x£©]=£®x-20£©Љю£їЄщЊЁ°∞„№јы»у=ЌтіпµкABЅљ÷÷–ЌЇ≈јы»уЇЌ+Ќтѕу≥«µкABЅљ÷÷–ЌЇ≈јы»у°±Љіњ…Ѕ–≥цЇѓ эєЎѕµ љ£ђ≤ҐЄщЊЁ±нЄсЄчЅњ µЉ “в“ењ…“‘»Јґ®„‘±дЅњ»°÷µЈґќІ£ї
£®2£©ЄщЊЁ„№јы»у≤їµЌ”Џ18140Ѕ–≥ц≤їµ» љ£ђљв≤їµ» љ£ђЄщЊЁ£®1£©„‘±дЅњ»°÷µЈґќІ£ђљш“ї≤љ»Јґ®x»°÷µЈґќІ£ђЄщЊЁxќ™’ы э£ђЉіњ…»Јґ®Јљ∞Є£Ѓ
љв£Ї£®1£©…иЈ÷≈дЄшЌтіпµк![]() –Ќ≤ъ∆Ј
–Ќ≤ъ∆Ј![]() Љю£®
Љю£®![]() £©£ђћо±н»зѕ¬£Ї
£©£ђћо±н»зѕ¬£Ї
|
| |
Ќтіпµк |
|
|
Ќтѕу≥«µк |
|
|
![]() £ђ
£ђ
’ыјн£ђµ√![]() £ђ
£ђ
Љі![]() єЎ”Џ
єЎ”Џ![]() µƒЇѓ эєЎѕµ љ «
µƒЇѓ эєЎѕµ љ «![]() .
.
£®2£©”…ћв“в£ђњ…µ√![]() £ђ
£ђ
љвµ√![]() £ђ
£ђ
°я![]() £ђ
£ђ
°а![]() £ђ
£ђ
°я![]() «’ы э£ђ
«’ы э£ђ
°а![]() £ђ79£ђ80£Ѓ
£ђ79£ђ80£Ѓ
°аЈ÷≈дЈљ∞Є”–»э÷÷£Ї
Јљ∞Є“ї£ЇЄшЌтіпµк![]() –Ќ≤ъ∆Ј78Љю£ђ
–Ќ≤ъ∆Ј78Љю£ђ![]() –Ќ≤ъ∆Ј62Љю£ђЄшЌтѕу≥«µк
–Ќ≤ъ∆Ј62Љю£ђЄшЌтѕу≥«µк![]() –Ќ≤ъ∆Ј2Љю£ђ
–Ќ≤ъ∆Ј2Љю£ђ![]() –Ќ≤ъ∆Ј58Љю£ї
–Ќ≤ъ∆Ј58Љю£ї
Јљ∞Єґю£ЇЄшЌтіпµк![]() –Ќ≤ъ∆Ј79Љю£ђ
–Ќ≤ъ∆Ј79Љю£ђ![]() –Ќ≤ъ∆Ј61Љю£ђЄшЌтѕу≥«µк
–Ќ≤ъ∆Ј61Љю£ђЄшЌтѕу≥«µк![]() –Ќ≤ъ∆Ј1Љю£ђ
–Ќ≤ъ∆Ј1Љю£ђ![]() –Ќ≤ъ∆Ј59Љю£ї
–Ќ≤ъ∆Ј59Љю£ї
Јљ∞Є»э£ЇЄшЌтіпµк![]() –Ќ≤ъ∆Ј80Љю£ђ
–Ќ≤ъ∆Ј80Љю£ђ![]() –Ќ≤ъ∆Ј60Љю£ђЄшЌтѕу≥«µк
–Ќ≤ъ∆Ј60Љю£ђЄшЌтѕу≥«µк![]() –Ќ≤ъ∆Ј0Љю£ђ
–Ќ≤ъ∆Ј0Љю£ђ![]() –Ќ≤ъ∆Ј60Љю£Ѓ
–Ќ≤ъ∆Ј60Љю£Ѓ

 ‘ƒґЅњм≥µѕµЅ–ір∞Є
‘ƒґЅњм≥µѕµЅ–ір∞Є°Њћвƒњ°њЊ≈ƒкЉґ э—І–°„йЊ≠єэ –≥°µч≤й£ђµ√µљƒ≥÷÷‘ЋґѓЈюµƒ‘¬ѕъЅњy£®Љю£© « џЉџx£®‘™/Љю£©µƒ“їіќЇѓ э£ђ∆д џЉџ°Ґ‘¬ѕъ џЅњ°Ґ‘¬ѕъ џјы»уw£®‘™£©µƒ»э„йґ‘”¶÷µ»зѕ¬±н£Ї
џЉџx£®‘™/Љю£© | 120 | 160 | 190 |
‘¬ѕъ џЅњy£®Љю£© | 260 | 180 | 120 |
‘¬ѕъ џјы»уw£®‘™£© | 5200 | 10800 | 10800 |
„Ґ£Ї‘¬ѕъ џјы»у![]() ‘¬ѕъ џЅњ°Ѕ£® џЉџ
‘¬ѕъ џЅњ°Ѕ£® џЉџ![]() љшЉџ£©
љшЉџ£©
£®1£©«уyєЎ”ЏxµƒЇѓ эљвќц љ£®≤ї“™«у–і≥ц„‘±дЅњµƒ»°÷µЈґќІ£©£Ѓ
£®2£©«уµ± џЉџќ™ґа…ў‘™ ±£ђ‘¬ѕъ џјы»у„оіу£ђ≤Ґ«у„оіујы»у «ґа…ў£њ
£®3£©”…”Џƒ≥÷÷‘≠“т£ђЄ√…ћ∆ЈљшЉџљµµЌЅЋm‘™/Љю![]() £ђ…ћЉ“єжґ®Є√‘ЋґѓЈю џЉџ≤їµ√µЌ”Џ180‘™/Љю£ђЄ√…ћµк‘ЏљсЇуµƒѕъ џ÷–£ђ‘¬ѕъ џЅњ”л џЉџ»‘»ї¬ъ„г£®1£©÷–µƒЇѓ эєЎѕµ£Ѓ»ф‘¬ѕъ џ„оіујы»у «14000‘™£ђ«уmµƒ÷µ£Ѓ
£ђ…ћЉ“єжґ®Є√‘ЋґѓЈю џЉџ≤їµ√µЌ”Џ180‘™/Љю£ђЄ√…ћµк‘ЏљсЇуµƒѕъ џ÷–£ђ‘¬ѕъ џЅњ”л џЉџ»‘»ї¬ъ„г£®1£©÷–µƒЇѓ эєЎѕµ£Ѓ»ф‘¬ѕъ џ„оіујы»у «14000‘™£ђ«уmµƒ÷µ£Ѓ