题目内容
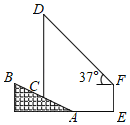
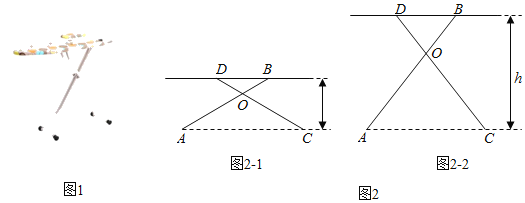
【题目】有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2﹣2).求该熨烫台支撑杆AB的长度(结果精确到lcm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
【答案】(1)55;(2)150cm.
【解析】
(1)作BE⊥AC于E,利用等腰三角形的性质求得∠OAC,然后解直角三角形即可求解;
(2)作BE⊥AC于E,利用等腰三角形的性质求得∠OAC,解直角三角形即可求解.
(1)过点B作BE⊥AC于E,
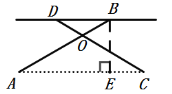
∵OA=OC,∠AOC=120°,
∴∠OAC=∠OCA=![]() =30°,
=30°,
∴h=BE=ABsin30°=110×![]() =55;
=55;
(2)过点B作BE⊥AC于E,
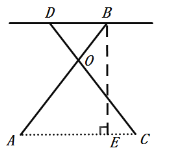
∵OA=OC,∠AOC=74°,
∴∠OAC=∠OCA=![]() =53°,
=53°,
∴AB=BE÷sin53°=120÷0.8=150(cm),
即该熨烫台支撑杆AB的长度约为150cm.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,

活动类型 | 频数(人数) | 频率 |
运动 | 20 | |
娱乐 | 40 | |
阅读 | ||
其他 | 0.1 |
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.