题目内容
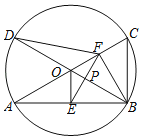
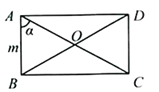
【题目】如图,矩形![]() 的对角线交于点O,已知
的对角线交于点O,已知![]() 则下列结论错误的是( )
则下列结论错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
根据矩形的性质得出∠ABC=∠DCB=90°,AC=BD,AO=CO,BO=DO,AB=DC,再解直角三角形判定各项即可.
选项A,∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,AC=BD,AO=CO,BO=DO,
∴AO=OB=CO=DO,
∴∠DBC=∠ACB,
∴由三角形内角和定理得:∠BAC=∠BDC=∠α,
选项A正确;
选项B,在Rt△ABC中,tanα=![]() ,
,
即BC=mtanα,
选项B正确;
选项C,在Rt△ABC中,AC=![]() ,即AO=
,即AO=![]() ,
,
选项C错误;
选项D,∵四边形ABCD是矩形,
∴DC=AB=m,
∵∠BAC=∠BDC=α,
∴在Rt△DCB中,BD=![]() ,
,
选项D正确.
故选C.

 阅读快车系列答案
阅读快车系列答案【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为![]() 次(
次(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用(元) | 350 | 650 | … | ||
方式二的总费用(元) | 200 | 400 | … |
(2)若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;
(3)当![]() 时,小亮选择哪种付费方式更合算.并说明理由.
时,小亮选择哪种付费方式更合算.并说明理由.