题目内容
【题目】在新冠病毒疫情防控期间,某校“停课不停学”,开展了网络教学.为了解九年级学生在网络学习期间英语学科和数学学科的学习情况,复课后从九年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制)的数据,通过对成绩数据的整理、描述和分析,得到了如下部分信息.
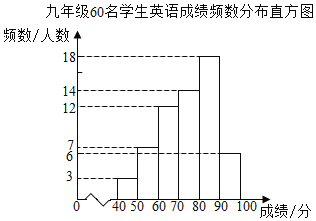
①英语成绩的频数分布直方图如图:
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100.)
②英语和数学成绩的平均数、中位数、众数如表:
学科 | 平均数 | 中位数 | 众数 |
英语 | 74.8 | m | 83 |
数学 | 72.2 | 70 | 81 |
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值是 .
(2)在此次测试中,李丽的英语成绩为74分,数学成绩为71分,该名学生成绩排名更靠前的学科是 .(填“英语”或“数学”),理由是 .
(3)若该校九年级共有500名学生,请你估计英语成绩超过77.5分的人数.
【答案】(1)76.5;(2)数学,该学生的成绩小于英语的中位数,而大于数学的中位数;(3)225人
【解析】
(1)根据统计图表求出总人数,判断中位数在70≤x<80这一组,根据中位数定义求解;
(2)可以从中位数角度进行分析;
(3)用样本的情况估计总体:英语成绩超过77.5分的人数为:500×![]() .
.
解:(1)∵英语成绩总人数为3+7+12+14+18+6=60,
∴中位数为第30、31个数据的平均数,而第30、31个数据均在70≤x<80这一组,
∴中位数在70≤x<80这一组,
∵70≤x<80这一组的是:70 71 72 73 73 73 74 76 77 77 77 78 79 79,
∴英语成绩的中位数为![]() =76.5,即m=76.5,
=76.5,即m=76.5,
故答案为:76.5;
(2)∵该学生的成绩小于英语成绩的中位数,而大于数学成绩的中位数,
∴这名学生成绩排名更靠前的课程是数学,
故答案为:数学,该学生的成绩小于英语的中位数,而大于数学的中位数;
(3)估计英语成绩超过77.5分的人数为500×![]() =225人.
=225人.

 口算能手系列答案
口算能手系列答案【题目】九年级数学小组经过市场调查,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如下表:
售价x(元/件) | 120 | 160 | 190 |
月销售量y(件) | 260 | 180 | 120 |
月销售利润w(元) | 5200 | 10800 | 10800 |
注:月销售利润![]() 月销售量×(售价
月销售量×(售价![]() 进价)
进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围).
(2)求当售价为多少元时,月销售利润最大,并求最大利润是多少?
(3)由于某种原因,该商品进价降低了m元/件![]() ,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
,商家规定该运动服售价不得低于180元/件,该商店在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是14000元,求m的值.
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆游泳的次数为![]() 次(
次(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
游泳次数 | 5 | 10 | 15 | … |
|
方式一的总费用(元) | 350 | 650 | … | ||
方式二的总费用(元) | 200 | 400 | … |
(2)若小亮计划今年游泳的总费用为2000元,选择哪种付费方式,他游泳的次数比较多;
(3)当![]() 时,小亮选择哪种付费方式更合算.并说明理由.
时,小亮选择哪种付费方式更合算.并说明理由.