题目内容
【题目】如图,Rt△ACB中,∠C=90°,AC=5cm,BC=2cm,点P从B点出发以1cm/s的速度沿CB延长线运动,运动时间为t秒.以AP为斜边在其上方构造等腰直角△APD.当t=1秒时,则CD=_____cm,当D运动的路程为4![]() cm时,则P运动时间t=_____秒.
cm时,则P运动时间t=_____秒.

【答案】4![]() 8
8
【解析】
连接CD,作DF⊥CB于F,DE⊥CA于E.首先证明AC+CB=![]() CD,延长即可解决问题;
CD,延长即可解决问题;
解:连接CD,作DF⊥CB于F,DE⊥CA于E.
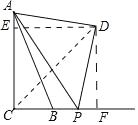
∵DA=DP,∠ADP=90°,
∴∠DAP=∠DPA=45°,
∵∠ACP+∠ADP=180°,
∴A,C,P,D四点共圆,
∴∠ACD=∠APD=45°,
∴∠ACD=∠DCF,
∵DE⊥CA,DF⊥CF,
∴DE=DF,
∵∠EDF=∠ADP=90°,
∴∠ADE=∠PDF,
∵∠DEA=∠DFP=90°,
∴△DEA≌△DFP(ASA),
∴AE=DF,
∵CD=CD,DE=DF,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=DF,
∴四边形ECFD是正方形,
∴AC+CP=EC+AE+CF﹣PF=2EC=![]() CD,
CD,
∵t=1s时,AC=5cm,CP=3cm,
∴CD=![]() =4
=4![]() (cm),
(cm),
当t=0时,CD=![]() =
=![]() ,
,
当D运动的路程为4![]() cm时,CD=4
cm时,CD=4![]() +
+![]() =
=![]() ,
,
∵AC+CP=![]() CD,
CD,
∴5+CP=15,
∴CP=10,
∴PB=8,t=8.
故答案为:4![]() ;8.
;8.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目







