题目内容
【题目】如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.
(1)说明△ADE≌△CFE;
(2)判断线段AB、CF、BD之间的数量关系,并说明理由.

【答案】(1)见解析;(2)AB=CF+BD,理由见解析
【解析】
(1)先由FC∥AB得∠A=∠FCE,∠ADE=∠F,进而利用AAS即可证得△ADE≌CFE;
(2)由△ADE≌CFE得AD=CF,再根据AB=AD+BD即可得到答案.
(1)证明:∵FC∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE与△CFE中:
∵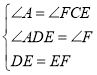 ,
,
∴△ADE≌△CFE(AAS).
(2)解:AB=CF+BD,理由如下:
∵△ADE≌△CFE,
∴AD=CF,
∵AB=AD+BD,
∴AB=CF+BD.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】甲、乙两位同学本学期11次考试的测试成绩如下:
甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(1) 他们的平均成绩和方差各是多少?
(2) 分析他们的成绩各有什么特点?
(3) 现要从两人中选一人参加比赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这次比赛?为什么?