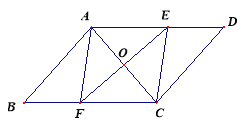
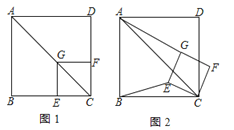
[题目]如图.已知点G在正方形ABCD的对角线AC上.GE⊥BC.GF⊥CD.垂足分别为点E.F.(1)求证:四边形CEGF是正方形,(2)将正方形CEGF绕点C顺时针旋转.如图所示.线段BE与DF是否相等?为什么? 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，已知点G在正方形ABCD的对角线AC上，GE⊥BC，GF⊥CD，垂足分别为点E，F.

（1）求证：四边形CEGF是正方形；

（2）将正方形CEGF绕点C顺时针旋转，如图所示，线段BE与DF是否相等？为什么？

【答案】（1）见解析

（2）相等，理由见解析.

【解析】

（1）先证明四边形CEGF是矩形，再根据邻边相等求出矩形CEGF是正方形；（2）相等，连接DF，证明△BCE≌△DCF，即可得证.

（1）在正方形ABCD中， BC⊥CD，∠ACB=∠BAC=45°

∵GE⊥BC，GF⊥CD，∴四边形CEGF是矩形

∵AB∥GE，∴∠EGC=∠BAC=∠ACB=45°，∴EG=EC，

∴矩形CEGF是正方形；

（2）相等；理由如下

连接DF，

∵将正方形CEGF绕点C顺时针旋转

∴∠BCE=∠DCF

又∵BC=DC,EC=FC，∴△BCE≌△DCF(SAS)

∴BE=DF.

练习册系列答案

	平均分（分）	中位数（分）	众数（分）	方差
（1）班	85	a	85	70
（2）班	85	80	b	c

（1）根据条形统计图中的信息，求上表中a，b，c的值；

（2）请你分析说明哪个班级的复赛成绩较好．

【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).

(1) 上述操作能验证的等式是__________________;

(2) 应用你从(1)得出的等式，完成下列各题：

①已知x24y2=12，x+2y=4，求x2y的值.

②计算：(1)(1)(1)…(1)(1).

【题目】如图，在平面直角坐标系中，平行四边形ABCD的边AD经过O点，A、C、D三点都在反比例函数的图像上，B点在轴的负半轴上，延长CD交轴于点E，连接CO.

若C（1,2）,D(2,1)，则为_______.

【题目】如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字“M”：

（1）请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；

（2）EF与A′B′有何位置关系？CC′与DH有何位置关系？

【题目】如图，已知AB=12，点C，D在AB上，且AC=DB=2，点P从点C沿线段CD向点D运动（运动到点D停止），以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF，连接EF，取EF的中点G，①△EFP的外接圆的圆心为点G；②四边形AEFB的面积不变；③EF的中点G移动的路径长为4；④△EFP的面积的最小值为8．以上说法中正确的有_____．

【题目】阅读下面材料：

2019年4月底，“百年器象——清华大学科学博物馆筹备展”上展出了一件清华校友捐赠的历史文物“Husun型六分仪”（图①），它见证了中国人民解放军海军的发展历程.六分仪是测量天体高度的手提式光学仪器，它的主要原理是几何光学中的反射定律.观察测者手持六分仪（图②）按照一定的观测步骤（图③显示的是其中第6步）读出六分仪加油弧标尺上的刻度，再经过一定计算得出观察测点的地理坐标.