Question

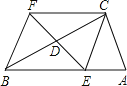
【题目】如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．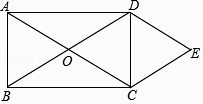
（1）求证：四边形OCED是菱形；
（2）若∠ACB=30°，菱形OCED的面积为10 ，求AC的长．

Answer 1

【答案】
（1）证明：∵CE∥BD，DE∥AC，

∴四边形OCED是平行四边形，

∵四边形ABCD是矩形，

∴AC=BD，OA=OC，OB=OD，∠ADC=∠ABC=∠BAD=90°，

∴OD=OC，

∴四边形OCED是菱形

（2）解：∵四边形OCED是菱形，

∴菱形OCED的面积=2△OCD的面积=△ACD的面积= ADCD=10 ，

∵∠ACB=30°，

∴∠BAC=60°，

∴∠DAC=30°，

∴AC=2CD，AD= CD，

∴ × CDCD=10 ，

解得：CD=2 ，

∴AC=2CD=4

【解析】（1）首先由CE∥BD，DE∥AC，可证得四边形CODE是平行四边形，又由四边形ABCD是矩形，根据矩形的性质，易得OC=OD，即可判定四边形CODE是菱形，（2）根据菱形OCED的面积=2△OCD的面积=△ACD的面积= ADCD=10 ，证出AC=2CD，AD= CD，得出 × CDCD=10 ，求出CD，即可得出答案．
【考点精析】通过灵活运用矩形的性质，掌握矩形的四个角都是直角，矩形的对角线相等即可以解答此题．