Question

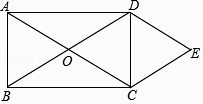
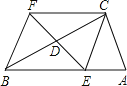
【题目】如图，在△ABC中，∠ACB=90°，且DE是△ABC的中位线．延长ED到F，使DF=ED，连接FC，FB．回答下列问题：

（1）试说明四边形BECF是菱形．

（2）当的大小满足什么条件时，菱形BECF是正方形？请回答并证明你的结论．

Answer 1

【答案】（1）见解析；（2）当∠A=45°时，菱形BECF是正方形．

【解析】（1）根据已知条件发现：可以证明四边形的对角线互相垂直平分即是一个菱形．

（2）菱形要是一个正方形，则根据正方形的对角线平分一组对角，即∠BEF=45°，则∠A=45°．

详（1）证明：∵DE是△ABC的中位线，

∴DE∥AC．

又∵∠ACB=90°，

∴EF⊥BC．

又∵BD=CD，DF=ED，

∴四边形BECF是菱形．

（2）解：要使菱形BECF是正方形

则有BE⊥CE

∵E是△ABC的边AB的中点

∴当△CBA是等腰三角形时，满足条件

∵∠BCA=90°

∴△CBA是等腰直角三角形

∴当∠A=45°时，菱形BECF是正方形．