题目内容
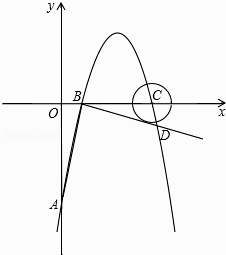
【题目】如图，抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0）两点，与y轴交于点C（0，3）．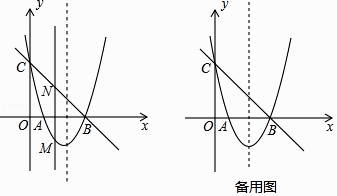
（1）求抛物线的解析式；
（2）若点M是x轴下方的抛物线上的一个动点，过点M作MN⊥x轴，交直线BC于点N，求四边形MBNA的最大面积，并求出点M的坐标；
（3）在抛物线上是否存在一点P，使△BCP为直角三角形？若存在，求出P点坐标，如果不存在，请说明理由．
【答案】
（1）
解：设抛物线解析式为y=a（x﹣1）（x﹣3），
把C（0，3）代入得a（﹣1）（﹣3）=3，解得a=3，
∴抛物线解析式为y=（x﹣1）（x﹣3），即y=x2﹣4x+3
（2）
解：如图1，设直线BC的解析式为y=kx+b，
把C（0，3），B（3，0）代入得 
，解得 
，
∴直线BC的解析式为y=﹣x+3，
设M（x，x2﹣4x+3）（1＜x＜3），则N（x，﹣x+3），
∴MN=﹣x+3﹣（x2﹣4x+3）=﹣x2+5x，
∴四边形MBNA的面积=S△ABM+S△ABN= 
ABMN= 2（﹣x2+5x）=﹣x2+5x=﹣（x﹣ 
）2+ 
，
当x= 时，四边形MBNA的面积最大，最大值为 ；
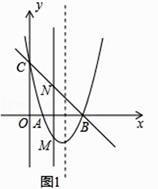
（3）
解：存在．
∵OB=OC，
∴△OBC为等腰直角三角形，
∴∠OBC=∠OCB=45°，
过B点作PB⊥BC交抛物线于P点，交y轴于Q点，如图2，则∠CBQ=90°，
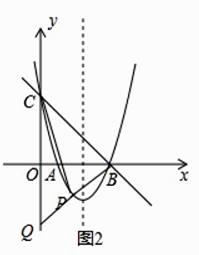
∵∠OBQ=45°，
∴△OBQ为等腰直角三角形，
∴OQ=OB=3，
∴Q（0，﹣3），
易得直线BQ的解析式为y=x﹣3，
解方程组 
得 
或 
，此时P点坐标为（2，﹣1）；
过C点作PC⊥BC交抛物线于P点，如图3，则∠PCB=90°，
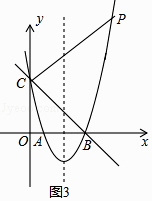
易得直线CQ的解析式为y=x+3，
解方程组 
得 
或 
，此时P点坐标为（5，8）；
当∠BPC=90°时，如图4，作PH⊥y轴于H，BF⊥PH于F，
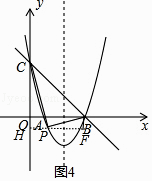
设P（t，t2﹣4t+3），
易证得△CPH∽△PBF，
∴ 
= 
，即 
= 
，
∴ 
= 
，
整理得t2﹣5t+5=0，解得t1= 
，t2= 
，此时P点坐标为（ ， 
）或（ ， 
），
综上所述，满足条件的P点坐标为（2，﹣1），（5，8），（ ， ），（ ， ）．
【解析】（1）设交点式y=a（x﹣1）（x﹣3），然后把C点坐标代入求出a即可；（2）如图1，先利用待定系数法求出直线BC的解析式为y=﹣x+3，设M（x，x2﹣4x+3）（1＜x＜3），则N（x，﹣x+3），则MN=﹣x2+5x，利用三角形面积公式得到四边形MBNA的面积= ABMN= 2（﹣x2+5x），然后根据二次函数的性质解决问题；（3）先判断△OBC为等腰直角三角形得到∠OBC=∠OCB=45°，讨论：过B点作PB⊥BC交抛物线于P点，交y轴于Q点，如图2，则∠CBQ=90°，判断△OBQ为等腰直角三角形得到OQ=OB=3，则Q（0，﹣3），易得直线BQ的解析式为y=x﹣3，通过解方程组 得此时P点坐标；过C点作PC⊥BC交抛物线于P点，如图3，则∠PCB=90°，同样方法可得易此时P点坐标；当∠BPC=90°时，如图4，作PH⊥y轴于H，BF⊥PH于F，设P（t，t2﹣4t+3），易证得△CPH∽△PBF，利用相似比得到 = ，于是通过约分整理得到t2﹣5t+5=0，然后解方程求出t即可得到此时P点坐标．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
