Question

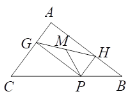
【题目】如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H．若点H是AC的中点，则 的值为 ．

Answer 1

【答案】
【解析】解：已知AD为角平分线，则点D到AB、AC的距离相等，设为h． ∵ = = = = ，
∴BD= CD．
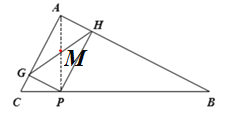
如图，延长AC，在AC的延长线上截取AM=AB，则有AC=4CM．连接DM．
在△ABD与△AMD中，

∴△ABD≌△AMD（SAS），
∴MD=BD= CD．
过点M作MN//AD，交EG于点N，交DE于点K．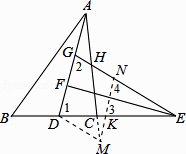

∵MN//AD，
∴ = = ，
∴CK= CD，
∴KD= CD．
∴MD=KD，即△DMK为等腰三角形，
∴∠DMK=∠DKM．
由题意，易知△EDG为等腰三角形，且∠1=∠2；
∵MN//AD，
∴∠3=∠4=∠1=∠2，
又∵∠DKM=∠3（对顶角）
∴∠DMK=∠4，
∴DM//GN，
∴四边形DMNG为平行四边形，
∴MN=DG=2FD．
∵点H为AC中点，AC=4CM，
∴ = ．
∵MN//AD，
∴ = ，即 ，
∴ = ．
故答案为： ．
方法二：
如图，有已知易证△DFE≌△GFE，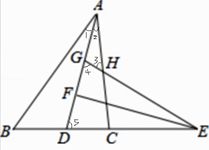

故∠5=∠B+∠1=∠4=∠2+∠3，又∠1=∠，
所以∠3=∠B，则可证△AGH∽△ADB
设AB=5a，则AC=4a，AH=2a，
所以AG/AD=AH/AB=2/5，而 AD=AG+GD，故GD/AD=3/5，
所以AG：GD=2：3，F是GD的中点，
所以AG：FD=4：3
解题关键是作出辅助线，如解答图所示：
第1步：利用角平分线的性质，得到BD= CD；
第2步：延长AC，构造一对全等三角形△ABD≌△AMD；
第3步：过点M作MN//AD，构造平行四边形DMNG．由MD=BD=KD= CD，得到等腰△DMK；然后利用角之间关系证明DM//GN，从而推出四边形DMNG为平行四边形；
第4步：由MN//AD，列出比例式，求出 的值．