题目内容
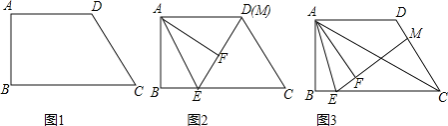
【题目】如图，将△ABC绕点C顺时针旋转m°得到△EDC，若点A、D、E在同一直线上，∠ACB=n°，则∠ADC的度数是（ ）
A. （m﹣n）°B. （90+n－
m）°C. （90－n+m）°D. （180﹣2n﹣m）°
【答案】B
【解析】
根据旋转的性质即可得到∠ACD和∠CAD的度数，再根据三角形内角和定理进行解答即可．
解：∵将△ABC绕点C顺时针旋转m°得到△EDC．
∴∠DCE=∠ACB=n°，∠ACE=m°，AC=CE，
∴∠ACD=m°-n°，
∵点A，D，E在同一条直线上，
∴∠CAD=
（180°-m°），
∵在△ADC中，∠ADC+∠DAC+∠DCA=180°，
∴∠ADC=180°-∠CAD-∠ACD=180°-（180°-m°）-（m°-n°）=90°+n°-m°=（90+n-m）°，
故选：B．
练习册系列答案
相关题目
