Question

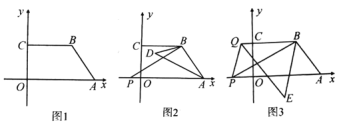
【题目】在平面直角坐标系中，四边形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上，顶点B 在第一象限，OA//CB．

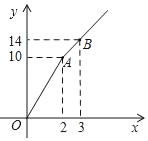
（1）如图 1，若点 A(6，0)，B(4，3)，点 M 是 y 轴上一点，且 SBCM SAOM ，求点 M的坐标；

（2）如图 2，点 P 是 x 轴上点 A 左边的一点，连接 PB，∠PBC 和∠PAB 的角平分线交于点D，求证：∠ABP+2∠ADB=180°；

（3）如图 3，点 P 是 x 轴上点 A 左边的一点，点 Q 是射线 BC 上一点，连接 PB、PQ，∠ABP和∠BQP 的平分线相交于点 E，求的值．

Answer 1

【答案】（1）（0，）或（0，）；（2）见解析；（3）2

【解析】

（1）首先根据题意可判断点M一定在点C的下方，接下来分类两种情况讨论：当0＜m＜3及m＜0时，根据SBCM SAOM及三角形的面积公式列出方程计算即可

（2）过点D作DH∥BC，根据平行线的性质可证得∠ADB＝∠DAO＋∠DBC，再根据角平分线可得∠PBC＋∠PAB＝2∠ADB，最后再根据两直线平行同旁内角互补即可得证；

（3）先设∠ABF＝∠EBG＝x，∠GQP＝∠EQB＝y，根据三角形的内角和及平行线的性质可分别证得∠BEQ－∠BAP＝x－y，∠BPQ－∠BEQ＝x－y，等量代换即可求得答案．

（1）解：设点M的坐标为（0，m），

∵点 A(6，0)，B(4，3)，

∴AO＝6，BC＝4，

∵SBCM SAOM，

∴点M一定在点C的下方，

当0＜m＜3时，

则，

解得，

∴点M的坐标为（0，），

当m＜0时，

则，

解得，

∴点M的坐标为（0，），

综上所述，点M的坐标为（0，）或（0，）；

（2）证明：如图，过点D作DH∥BC，

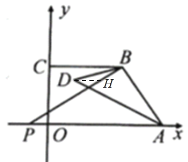
∵DH∥BC，OA∥BC，

∴DH∥OA，

∴∠HAD＝∠DAO，

∵DH∥BC，

∴∠HAB＝∠DBC，

∴∠ADB＝∠HAD＋∠HAB

＝∠DAO＋∠DBC，

∵DB、DA分别平分∠PBC、∠PAB，

∴∠PBC＝2∠DBC，∠PAB＝2∠DAO，

∴∠PBC＋∠PAB＝2(∠DBC＋∠DAO)

＝2∠ADB，

∵OA∥BC，

∴∠PAB＋∠ABC＝∠PAB＋∠PBC＋∠ABP＝180，

即2∠ADB＋∠ABP＝180°；

（3）解：如图，

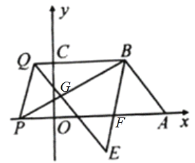
∵∠ABP和∠BQP的平分线相交于点E，

∴设∠ABF＝∠EBG＝x，∠GQP＝∠EQB＝y，

∵OA∥BC，

∴∠AFB＝∠EBQ，

∴180°－(∠ABF＋∠BAP)＝ 180°－(∠BEQ＋∠EQB)

∴∠ABF＋∠BAP＝∠BEQ＋∠EQB，

即：x＋∠BAP＝∠BEQ＋y，

∴x－y＝∠BEQ－∠BAP，

∵∠EBG ＋∠BEQ＋∠BGE＝∠GQP＋∠BPQ＋∠PGQ＝180°，∠BGE＝∠PGQ，

∴∠EBG ＋∠BEQ ＝∠GQP＋∠BPQ，

即：x＋∠BEQ＝y＋∠BPQ，

∴x－y＝∠BPQ－∠BEQ，

∴∠BPQ－∠BEQ＝∠BEQ－∠BAP，

即∠BPQ＋∠BAP＝2∠BEQ，

∴，

∴的值为2．